【创作培育计划】“拉马努金复生才能解决”：E₈格与装球问题

乌克兰数学家维亚佐夫斯卡获得2022年菲尔兹奖，获奖理由是“证明E8给出8维全等球体最密堆积，以及对相关极值问题和傅里叶分析中插值问题的进一步贡献。”她的获奖工作可谓是“菲尔兹奖少有的接地气的成果”——从研究问题本身来说，她所研究的是8维装球堆积密度最大的问题，我们很容易理解三维空间中的装球问题；而获奖理由中所叙述的“格”也并不复杂。本文将用基本的数学知识介绍相关概念，特别是E8格的特殊意义，它又如何与装球问题联系起来。相关研究源远流长，而现在则是一次直接了解现代数学前沿的绝好机会。

撰文 | 倪忆（加州理工学院数学系教授）2022年7月5日，乌克兰数学家马林娜·维亚佐夫斯卡（Maryna Viazovska）获得菲尔兹奖。她获奖的主要工作是解决了8维空间中的装球问题：当8维空间中的球按照E8格的方式堆积起来时，装球密度最大。她还与人合作解决了24维空间中的装球问题，这时最大密度是以利奇格的堆积方式取得。

这一获奖工作可谓是菲尔兹奖里少有的接地气的成果，普通人都能理解她到底证明了什么。从数学上说，她的获奖工作再次向世人展示了E8格（以及利奇格）的重要性。那么，什么是E8格？它又如何同装球问题联系起来的呢？

什么是格？

格（lattice），是大数学家高斯（Carl Friedrich Gauss，1777-1855）所定义的一个数学概念。我们拿二维格作为例子来说明格的定义。取一个平行四边形，将它平行移动，可以得到无数个同样形状和大小的平行四边形，使得它们铺满平面。这些平行四边形的顶点构成的集合就叫作一个二维格。

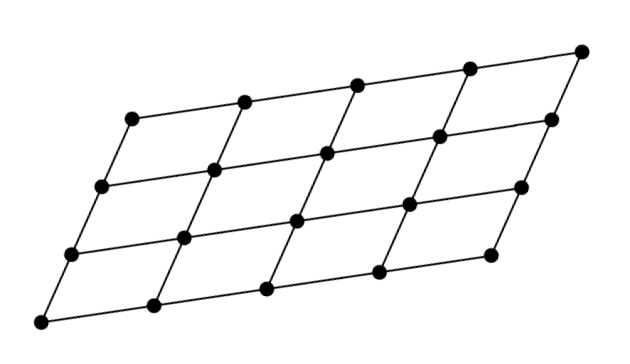
平行四边形的顶点构成一个二维格

最常见的二维格由平面上所有整点组成，也就是说，这些点在直角坐标系里的横纵坐标都是整数。相应于这一格的平行四边形就是边长为1的正方形。我们管这个格叫作正方形格。

正方形格

如果平行四边形由两个边长为的等边三角形拼成，得到的格称为六边形格。

六边形格

类似于平面格，在三维空间，我们可以用平行六面体平移堆满空间，平行六面体的顶点的集合就是一个三维格。

当这个平行六面体是正方体时，对应的格叫作简单立方格。在简单立方格的基础上，再添加每个立方体各个面的中心，得到的格叫作面心立方格。

在许多晶体中，原子或者分子就是按照格的方式来排列，所以化学家们经常要跟格打交道。例如 α相的固态钋的晶体结构是简单立方结构，而常见的氯化钠（食盐）晶体里的氯原子是按照面心立方格方式排列。

不过，晶体学中所说的lattice跟我们这里的格不完全一样，例如晶体学中常见的密排六方晶格就不是我们所说的格。我们所说的格，在晶体学中被称为Bravais lattice。

高维空间中的格可以类似地定义。不过，为了叙述的简洁，我们采用线性代数的语言。

如果读者学过线性代数，应该知道n维欧氏空间可以看作一个向量空间，或者说线性空间。这个向量空间的一组基就是n个向量使得向量空间中任何一个向量可以用唯一的方式表示为这n个向量的实系数线性组合，即的形式，其中每一个系数ki都是实数。

现在给定一组基，如果我们限定上式中的系数ki都是整数，那么这样得到的所有向量的集合就叫作一个格。格中的向量（也可看作空间中的点）则称为格点。

独一无二的E8格我们要谈到的E8格是一个非常特殊的8维格。为了说明它为什么特殊，我们需要一些进一步的关于格的概念。

如果一个格中任何两个向量的内积都是整数，那么这个格就被称为整格。在这个定义里，当两个向量是同一个向量时，它们的内积就是向量长度的平方。所以整格中任何一个向量长度的平方都是整数。换句话说，整格中任两个格点之间距离的平方都是整数。

在平面上，整格也可以用相关的平行四边形的几何来定义：如果平行四边形每条边长度的平方都是整数，并且两条对角线长度的平方差是4的整数倍，那么这个格就叫作整格。

读者可以验证前面提到的正方形格和六边形格都是整格。

在一个整格中，如果每个向量的长度的平方都是偶数，那么这个格叫作偶格。在二维格里，前述条件等价于要求平行四边形每条边长度的平方都是偶数。正方形格边长的平方是1，所以正方形格不是偶格。六边形格边长的平方是2，所以六边形格是偶格。

在格定义中，作为基的这组向量构成一个方阵。如果这个方阵的行列式是±1，这个格就叫作一个幺模格。在二维的时候，上面这个方阵的行列式的绝对值就是相应平行四边形的面积；在三维时，行列式的绝对值是相应平行六面体的体积。

正方形格对应的正方形面积是1，所以正方形格是幺模格。六边形格对应的菱形的面积是√3，所以六边形格不是幺模格。

总结一下，**正方形格是幺模格，但不是偶格；六边形格是偶格，但不是幺模格。**那么，平面上有没有一个整格，既是偶格又是幺模格呢？

不难证明，这样的平面格不存在。事实上，假设平行四边形两组对边的长度的平方分别是a和b，两条对角线的长度的平方差是4d，那么平行四边形的面积就是。如果这个格是幺模格，那么如果这个格还是偶格，那么a和b都是偶数，这样d2=ab-1被4除的余数是-1，跟d是整数矛盾。

平面上没有幺模偶格，在高维有吗？我们可以考察三维、四维…… 要一直到八维才会出现第一个幺模偶格，这就是E8。

E8格可以这样定义：它由里满足如下两个条件的点组成：第一个条件是，全部8个坐标的和是偶数；第二个条件是，所有坐标要么都是整数，要么都是半整数（即某个奇数的一半）。

对于E8格，可以取这样一组基：这组基的特点是，每个向量长度的平方都是2，并且两两之间的内积可以用如下的图来表示：

上图里，如果两个顶点之间连有一条边，那么对应的两个向量的内积就是-1，否则两个向量的内积是0。这个图在李代数的根系分类中记作E8，所以相应的格称为E8格。

可以证明，幺模偶格的维数一定是8的倍数。所以只是在8、16、24、32…这些维数才有幺模偶格。事实上，在8维时，E8在同构意义下是唯一的幺模偶格。

另外一个著名的幺模偶格是24维的利奇格（Leech Lattice）。康威（John Horton Conway，1937-2020）曾经在研究利奇格的对称群时发现了3个散在单群。

E8格是数学里非常重要的一个对象，它频繁出现在群论、李代数、拓扑、模形式、弦理论等数学和物理领域中，编码理论中的汉明码（Hamming code）也跟E8格有关。

1962年，米尔诺（John Milnor）因为发现七维球面上的“怪异”微分结构而获得菲尔兹奖。利用E8可以构造出七维球面上的全部28个不同的微分结构。

1983年，弗里德曼（Michael Freedman）因证明四维庞加莱猜想而获得菲尔兹奖。弗里德曼实际上完成了单连通四维闭流形的拓扑分类。他的结果的一个推论就是，存在没有微分结构的四维流形。这个流形的构造就利用了E8。

不过，尽管好几位菲尔兹奖得主的获奖工作都与E8有关，今年E8还是第一次直接出现在菲尔兹奖获奖工作中。这次E8大显身手的舞台是装球问题。

开普勒猜想装球问题（sphere packing problem）是一个来源于日常生活的问题：把同样大小的球堆积起来，怎么样才能使得密度最大？一种自然的堆积方式是，先把球铺排一层，使得每个球周围恰好有六个球与之相切。然后在适当的空隙上方再放置一层球，在适当的空隙下方也可以放置一层球。依此类推，铺至整个空间。容易算出，这种方法得到的堆积密度是著名天文学家开普勒（Johannes Kepler，1571-1630）在1611年的一篇文章中猜测，这样堆积的密度是最大的。这就是开普勒猜想。

动手试一下，就会发现，实现这一密度的堆积方法有很多种。在下图里，圆圈表示放好的一层球。接下来的一层球如何放有两种选择：既可以放到红点所在空隙的上方，也可以放到蓝点所在空隙的上方。同样地，放好这一层后，再接下来一层又有两种选择。以此类推，可以看出，能取得最大密度的堆积方式有无穷多种。

可以说，每一个卖橘子的商贩都知道这种堆积能取得最大密度，但这一事实的证明却花了人类四百多年时间。

装球问题的困难在于，在一个小范围里可以有一种装球方式，使得这个小范围里的堆积密度大于。可一旦你想把这种装球方式扩充到整个空间，堆积密度必然会小于。所以装球问题不可能用简单的局部分析来解决。

我们可以看一个例子。在达到最大堆积密度的装球方式里，每个球周围恰好有12个球跟它相切。但是，这12个球并没有以最均匀的方式分布。上图是另外一种在（红色）小球周围放置12个与之相切的（蓝色）小球的方式，蓝球的球心构成正十二面体十二个面的中心。跟达到最大堆积密度的堆积方式相比，这种堆积方式的12个球分布得更均匀，局部上有着更高的对称性。可以算出，红球附近的堆积密度是0.7546···，比···略大。但是，你没法把这一堆积方式扩充到整个空间，使得每个小球周围都有这么12个均匀分布的小球！所以0.7546···这一密度在整个空间中是不能实现的。

有同学会问了：“都是跟12个小球相切，为什么分布越均匀局部密度越大？”可以这么想：假设有四条彪形大汉，从东南西北四个方向围着你，是不是压迫感十足？现在如果这四条大汉跟你的距离不变，但改成半包围形势，留出一个方向让你跑路，是不是压迫感没那么强了？这就是为什么分布越均匀，局部密度就越大。当然，局部密度在数学上有严格定义，我们就不在这里给出了。

1831年，高斯证明了，如果把球按照格的方式堆积起来，那么最大密度是。但这离开普勒猜想的解决还差得很远，因为达成最大密度的堆积完全可以不是格的方式。事实上，在无穷多种密度达到的堆积中，只有一种堆积的球心构成格。这个格就是前面提到的面心立方格。（密排六方晶格同样达到最大密度，但这不是我们所说的格。）

匈牙利数学家拉斯洛‧费耶斯‧托特（László Fejes Tóth，1915-2005）在1953年提出了一个方法，只需要进行有限多次计算就能够验证开普勒猜想。但这个计算量非常大，以当时计算机的能力根本无法完成。1998年，美国数学家黑尔斯（Thomas Hales）使用费耶斯‧托特的方法，在计算机辅助下给出了开普勒猜想的一个证明。他将开普勒猜想划分为大约十万个线性规划问题，每个问题有200个左右的变量，1000个左右的限制条件，可以用计算机解答。他的论文有270页，此外还有3 GB的数据，以及超过四万行计算机程序。很显然，这样的证明不是人类所能够检验的。

黑尔斯将他的论文投到了《数学年刊》，拉斯洛‧费耶斯‧托特的儿子加博尔‧费耶斯‧托特（Gábor Fejes Tóth）率领的一个12人团队负责审核论文。经过四年的艰苦工作，加博尔‧费耶斯‧托特的团队报告说他们有99%的把握认为证明是对的，但他们无法确认所有计算的正确性。最终，《数学年刊》发表了黑尔斯原始论文的数学理论部分，有120页。其余偏重计算的部分则分成若干篇论文发表在《离散计算几何》杂志上。这种做法对于《数学年刊》这样的顶级杂志来说是相当不寻常的。

尽管黑尔斯的论文已经发表在权威杂志上，数学界仍然有很多人对其证明抱持着怀疑态度。于是黑尔斯又花了十几年时间，率领团队在2014年给出了一个“形式化证明”（formal proof）。也就是说，这个证明可以由计算机读取，并用现成的证明辅助软件来自动检验每一步逻辑推理是否正确。介绍这一形式化证明的论文于2017年发表在《数学论坛 Pi》上，算是终结了对开普勒猜想证明正确性的质疑。

虽说开普勒猜想已经得到了证明，但这个证明并不是大部分数学家想要的。黑尔斯的证明需要用计算机作海量的计算，检验证明也需要用计算机。雅可比（Carl Gustav Jacob Jacobi，1804-1851）曾说过：“科学的唯一目的是为了人类心智的荣耀。”如果人类的心智永远不能理解这个证明，又谈何荣耀呢？

8维和24维的突破开普勒猜想研究的是三维空间里的装球问题。在任意维数的空间中，也可以提出类似的装球问题，即同样大小的球堆积起来何时密度最大。这里一个“球”就是空间中到一个固定点（即“球心”）的距离不超过一个固定长度（即“半径”）的点的集合。例如直线上的一维“球”就是一条线段，平面上的二维“球”就是一个圆盘。

一维的装球问题是平凡的：最大密度是1，我们只需要把线段一个个接起来就能填满直线。

二维的装球问题比较初等，很容易想到，当圆盘的中心组成一个六边形格时，密度最大。这一事实的第一个证明是挪威数学家图厄（Axel Thue，1863-1922）在1890年给出的。

在2016年之前，1、2、3这三个维数是装球问题得到完全解决的仅有的三个维数。

在二维和三维，密度最大的堆积很容易猜出来，尽管证明并不容易。到了高维空间中，密度最大的堆积通常很难猜出来。但是，8维和24维这两个维数比较特殊。在这两个维数存在着E8格和利奇格这两个高度对称的格，人们很自然地会猜测，当球心组成E8格或者利奇格时，堆积密度最大。

2003年，微软研究院的科恩（Henry Cohn）和哈佛大学的埃尔基斯（Noam Elkies）发展了一种新方法来估计高维空间中最大的堆积密度。他们的方法需要用到一个辅助函数f(x)，使得f(x)与它的傅立叶变换满足一定的条件。这时最大堆积密度的上限就能用给出。使用这种方法，科恩和他的合作者证明了8维空间中最大堆积密度不超过E8格堆积密度的1+10-14倍，而24维空间中最大堆积密度不超过利奇格堆积密度的1+1.65×10-30倍。这已经非常接近于证明E8格和利奇格的堆积密度最大了，但还不是证明。

要想同时控制f(x)与它的傅立叶变换并不容易。这一事实在物理上的表现就是海森堡（Werner Heisenberg，1901-1976）的不确定性原理。科恩和埃尔基斯曾经向许多数学家宣传过他们的工作，期望他们需要的辅助函数已经悄悄地存在于世界的某一角落。但他们和其余所有顶尖专家花了十几年时间都没能找到合适的辅助函数。黑尔斯认为这一辅助函数是存在的，但是“需要拉马努金复生才能找到它。”（注：黑尔斯所说的原文为I felt that it would take a Ramanujan to find it，并未明显包含“复生”之意。）
拉马努金（Srinivasa Ramanujan，1887-1920）是一位自学成才的印度数学家。他凭直觉写下了大量复杂而优美的数学公式，却无法解释它们的来历，而将其归结于神启。

维亚佐夫斯卡不是拉马努金，更没有得到神启。她花了两年时间，利用数论里的模形式，为E8构造出了正确的辅助函数。她的论证没有用到非常抽象的现代数学知识，而是展示出了高超的数学技巧。毫不夸张地说，十九世纪的那些数学大师们就可以理解并欣赏她的工作。

她的构造，建立在两位跟拉马努金同等级别，但远没有那么出名的数学天才的工作基础之上，并加上了她自己的独特贡献。

这里所说的第一位天才是德国数学家艾森斯坦（Gotthold Eisenstein，1823-1852），他是高斯最钟爱的弟子。高斯曾经在一封给亚历山大·冯·洪堡（Alexander von Humboldt，1769-1859）的信中称赞艾森斯坦是一个世纪中只出现几位的天才。据高斯另外一位学生莫里兹·康托尔（Moritz Cantor，1829-1920）的记载，高斯甚至说过：“只有三位超越时代的数学家，那就是阿基米德、牛顿、和艾森斯坦。”这些言论或许不无夸大之处，但艾森斯坦在他的短暂一生中无疑取得了令人瞩目的成就，这一点很像拉马努金。

艾森斯坦最重要的工作是提出了艾森斯坦级数。艾森斯坦级数是数论里模形式的重要例子。第二位天才同样是一位德国数学家，就是雅可比，前面引用过他的名言。雅可比是历史上计算能力最出色的数学家之一，著名数学史家贝尔（Eric Temple Bell，1883-1960）在《数学精英》一书中把他称为“伟大的算学家”。哈代（Godfrey Harold Hardy，1877-1947）认为，拉马努金对代数公式和无穷级数的直觉，历史上只有欧拉（Leonhard Euler，1707-1783）和雅可比才能与之相比。可见雅可比在这方面的能力是多么的杰出。

雅可比定义了四个雅可比θ函数，并且证明了关于它们的一系列恒等式。最基本的一个θ函数是维亚佐夫斯卡本人的重要贡献是定义了一个新的积分变换。所谓积分变换，就是从一个函数出发，通过积分得到一个新的函数。著名的积分变换有傅立叶变换和拉普拉斯变换。维亚佐夫斯卡从最初几个艾森斯坦级数E2, E4, E6出发，经过简单的加减乘除，再用上她新定义的积分变换，得到了一个函数a(x)，其傅立叶变换就是它本身。用类似方法，从三个雅可比θ函数出发，能得到一个函数b(x)，其傅立叶变换是它的相反函数-b(x)。最终的辅助函数则是a(x)和b(x)适当的线性组合。

维亚佐夫斯卡解决8维装球问题的论文于2016年3月在网上发表，只有24页。在她把论文放上网的当天晚上，科恩就给她发信祝贺，并问能否把这一方法推广到维空间。他们两人与另外三位数学家合作，在7天后发布了一篇12页的论文，证明了利奇格的堆积在24维空间中是密度最大的。这一团队后来又写了一篇100页的论文，证明E8格和利奇格具有“泛最优性”。也就是说，如果把无穷多个互斥的粒子放到8维或24维空间中，使得它们之间的斥力满足一定条件，那么E8格或利奇格就是能量最低的摆放方式。

迄今为止，装球问题只在1、2、3、8、24这五个维数得到解决，而泛最优性只在1、8、24这三个维数得到解决。为什么8维比4、5、6、7维更容易？即便这一领域的专家们也难以给出一个满意的回答。这其中或许有着非常深刻的原因。

有人会问：“我们生活的空间就是三维的。研究二维和三维的装球问题还可以说有现实意义，研究高维的干什么？”事实上，人们研究装球问题并不完全出于数学上的兴趣。三维空间的装球问题跟材料科学密切相关，高维的装球问题则在通信和编码理论中起到重要的作用。

从数学上说，装球问题不是一个孤立的问题，它跟数论、调和分析、线性规划等许多数学分支都有联系。在研究这一问题中发展出来的方法，可以被运用到别的数学领域。从这一意义来说，装球问题就像一只下金蛋的鹅。维亚佐夫斯卡所发展的方法，正是这只鹅下的诸多金蛋之一。菲尔兹奖的表彰，一定程度上是对金蛋成色的肯定吧。

出品：科普中国创作培育计划