[科普中国]-在吹泡泡史上，这些科学家留有姓名-

肥皂泡从吹出到破裂，仅存在寥寥几秒。但在历史长河中，却有无数学者沉醉于这转瞬即逝的魅力，试图解答泡泡所带来的迷思。

表面张力与长寿泡泡

英国实验物理学家波易斯，设计过一个也许是受众最广的肥皂泡实验。

1889年圣诞节期间，他进行了几次公开演讲，给青少展示肥皂泡实验。其中一个实验是这样的：把一个圆环放在肥皂水中一抄，就形成了一层肥皂膜；如果在环中系上一根线（并且其中一段是双线），就会形成三个膜，把双线中的膜捅破，双线包裹的面积就自然地形成了一个圆形。

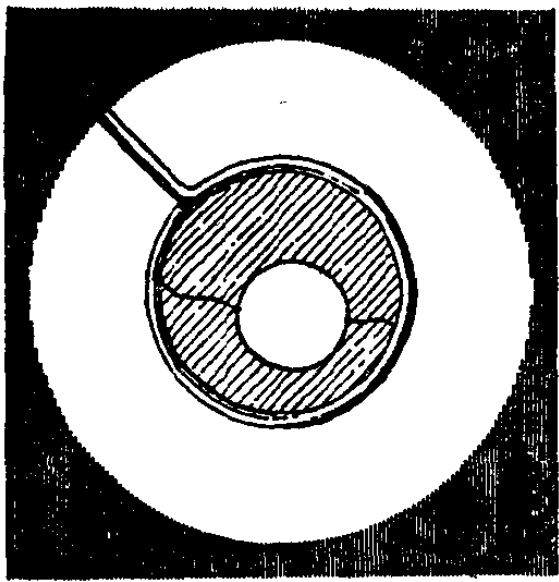（两根线被拉成圆形蕴含了深刻的数学和物理 | 《肥皂泡和形成它们的力》）

这一实验直观地演示了表面张力使液体表面积达到最小的过程，这也是空中肥皂泡成为球形的原因。

但表面张力对于肥皂泡的意义，远不止于此——它可是肥皂泡的救命稻草。当肥皂泡的液膜受到扰动而局部变薄时，这部分区域表面张力会变大，并对周围液体产生更大拉力。于是，液体会被自然拉向变薄处，完成自我修复。这种现象名为马拉高尼效应（Marangoni Effect）。

（看似脆弱的肥皂泡，每时每刻都在拼命对自己修修补补，想想有些悲壮…… | pixabay）

低温气体的研究先驱詹姆斯·杜瓦，以发明了保存液态空气的杜瓦瓶闻名于世。在人生的最后20年，他沉浸于肥皂泡表面张力的研究。

他创造了一个惊人的记录。通过把泡泡精心保存于特制瓶中，减少与空气杂质的接触，杜瓦将一个泡泡保存了三年。

想必，瓶中的泡泡也在感受着马拉高尼效应的力量。

哪里都有牛顿

不过肥皂泡最让人着迷的，还是那变幻不定的色彩。

阳光下的泡沫，为啥是彩色的？这个问题的答案来自于牛顿。

牛顿一生，光辉灿烂，数学、力学、光学、天文，全面开花。而在其光学成就中，有一项名为 “牛顿环” 的研究成果，可以解释泡泡为什么五彩斑斓。

肥皂膜本身是无色的。阳光在肥皂膜的上下两个表面分别反射，并发生干涉。阳光是由不同波长的可见光组成。在膜的某一处，恰好两束反射光中红光相互抵消，这处就呈现蓝绿色；在另一处，红光又可能得到加强。再有，肥皂膜的厚度并不均匀，并随着气流、重力的扰动，膜厚度也一直变化。于是，整个肥皂泡就呈现出了不断变换的五彩斑斓。水面上漂浮的油膜，镜片或珍珠的表面都会出现这种现象。

（镜片上发生的牛顿环现象 | wiki）

老勋爵的问题

当然，牛顿并不是靠吹泡泡发现牛顿环的。不过，倒是有不少学者在吹肥皂泡中发现了新天地。

热力学奠基人，英国物理学家开尔文勋爵，就是其中一位。

开尔文曾说：“ 如果你吹一个肥皂泡并进行观察，你可以对它进行一生的研究，并从中获得一个又一个物理定律。” 1887年，开尔文的侄女特意到乡下去看望这位老爵士。打开大门，眼前的画面是这位大学者在开心地吹着泡泡。

沉迷于肥皂泡的开尔文勋爵，曾提出过一个问题：如果将空间划分成很多个部分，保证接触面积最小，这些部分应该是什么形状？

这个问题被后世称为“ 开尔文问题 ”。

在二维平面中，开尔文问题已经被蜜蜂解答了。六角形的蜂巢结构，就是平面上效率最高的堆积方式。当然，蜜蜂们没有什么数学基础，它们这么筑巢，只是为了省点蜂蜡——这就是大自然的智慧！

至于三维空间的开尔文问题，老勋爵自己给出的答案是截角八面体，它由八个正六边形和六个正方形组成。

开尔文认为，用这种结构填充空间最为高效。这个答案显然受到了肥皂泡的启发。

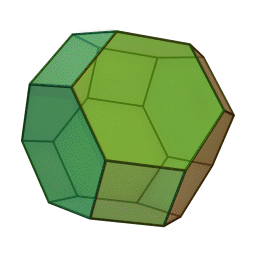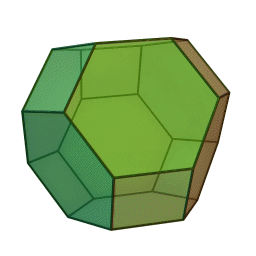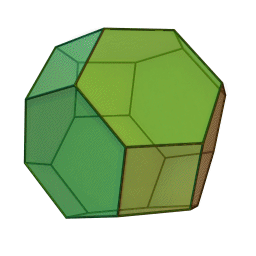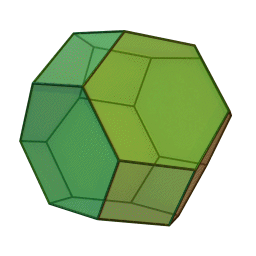
（截角八面体（6个正方形和8个正六边形组成）和其空间排布 | wiki）

虽然开尔文对他的这一说没有给出严谨的证明，但在随后100多年里，大部分人相信出题人的回答就是这一问题的最优解。

超越开尔文——威尔―弗兰气泡

直到1993年，开尔文的泡泡破了。

爱尔兰物理学家丹尼斯·威尔和罗伯特·弗兰提出了一种新设计，超越了开尔文结构。

这种名为“ 威尔―弗兰气泡 ”的结构，包含12面体和14面体两种单元。用威尔―弗兰气泡填充空间，可以比开尔文的方法节约0.3%的原料。

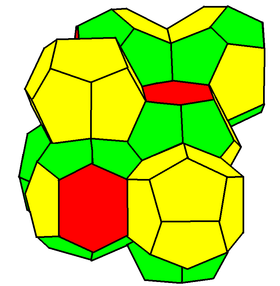（威尔-弗兰气泡结构 | wiki）

值得一提的是，威尔-弗兰气泡正是北京奥运会游泳中心（水立方）的设计灵感。因为借鉴了这一模型，大大减少了“水立方”需要的钢材数量，整个建筑主体只用了6700吨钢结构就建成了（和正常水平相比，节省了多少？）。

（水立方借鉴了威尔-弗兰气泡模型 | wiki）

不过，威尔-弗兰气泡是否为 “开尔文问题”的最终解，我们现在也不能下定论，只能寄希望于那些吹着泡泡的科学家们多多加油。

普拉托也有一个问题

和开尔文一样，比利时物理学家普拉托也是一位沉迷吹肥皂泡的大师，他甚至写下了长达450页关于泡泡的专著《仅在于分子作用力下的液体静力学和实验》（Statique expérimentale et théorique des Liquides soumis aux seules Forces moléculaires，1873）。

普拉托也在吹泡泡中发现了一个问题：在数学上在给定边界曲线的情况下，如何求出最小曲面。这一问题也被命名为“ 普拉托问题 ”。

为了解答这一问题，需要涉及到几何学的很多高深理论。但在生活中，只要你拿个铁丝弯成边界，沾点肥皂水，你吹出的泡泡就是普拉托问题的解。

（沉迷泡泡研究的普拉托（Joseph Plateau） | New Scientist）