[科普中国]-我想让几何机器人摸爬滚打，成为美丽的强者造福人类｜姚燕安

能抢险救援，能探测星球，甚至维护世界和平…“几何机器人“究竟能有多强大的力量？北京交通大学机械与电子控制工程学院教授、北京交通大学机器人研究中心执行副主任姚燕安和我们分享：《我想让几何机器人摸爬滚打，成为美丽的强者造福人类》。

以下为姚燕安演讲实录：

我是姚燕安，来自北京交通大学机械与电子控制工程学院和北京交通大学机器人研究中心。

机器人，大家应该都不陌生。传统的机器人概念，是人形机器人（又名两足机器人、足式机器人或仿人型的机器人），有两条腿。也包括机器动物，比如著名的美国波士顿动力公司开发了一种仿大狗的机器人，叫做Big Dog。再广义一些，也包括仿蛇形的机器人。

从机器人研究专家角度来看，其实还有一种仿生形的机器人——轮式、履带式或者球形的小车，给它装上摄像头，它就有一定对环境感知的能力；再装上车载的计算机，它就能够进行自动决策和判断。

所以，机器人是一个更为广义的家族概念。

“几何机器人”是我自己起的名词，是一类完全新概念的机器人 。

这是我们一款三角形的机器人。三角形的结构很稳固，但我把三角形机器人做成可变形，三条边都可以伸缩，三个角都可以变化。然后给它装两只脚，它就变成了一个可以步行的三角形机器人。

这是一款四边形机器人。大家能注意到，它一会变成正四边形，一会变成平行四边形，在地上滚动。

轮子大家应该都很熟悉，如果说它是世界上最伟大的发明，估计大多数人也没有异议。轮子的几何形状其实很简单，就是个圆形或者圆柱体。但有了轮子，汽车就可以用来载重，可以高速行驶，整个推动了人类文明的进步。所以我一直开玩笑，说这个能滚动的四边形机器人是我最伟大的发明。

轮子适合很硬的路面，比如高速公路；但是它不适合松软的野外路面。这种四边形的机器人，以及我们后面会看到更复杂的可以变形的机器人，可以适应更复杂的地形。

我把这一类机器人叫做多边形机器人，这里展示的是六边形机器人。它是个六边形，但是可以一会变成三角形，一会变成四边形，还可以往左滚，往右滚。

这是我的孩子刚刚上初中的时候，我们给拍的录像，他现在已经上大学了。画面中他在指挥这个机器人，一会让它向左走，一会让它向右走，像交警在指挥交通一样。

这就有了一个很重要的机器人的概念： 变形机器人 。它的形态可以变化。

在初中，我们就学了平面几何，上面展示的是一部分平面几何的机器人；而高中，我们开始学立体几何了，所以也设计了一些立体几何机器人。

这是四面体机器人。当它站得比较正的时候，是一个标准的四面体。四面体由四个三角形构成，我把这四个三角形都做成可变形的三角形，就变成一个可以变形的四面体机器人。这样，它整体的高度和宽度就可以变化， 很适合进行一些摸爬滚打的活动，比如爬山、钻洞 。

还有更复杂的。这是双正交的四边形。

这个叫削棱截角多面体。

这个是双三角锥，它由两个四面体组合构成。

我们实验室还开发了更为复杂的变形机器人。

有一种拓扑几何，是拓朴学跟几何学的融合，是研究形状在变化过程中性质的一门学科。像我们也设计了几款拓扑几何的机器人。

像这款机器人，它是个椭球形，但是可以展开变成一个多面体。大家可能会很奇怪，怎么用啊？现在是把它做成炮弹。 用炮弹把它打出去，让机器人展开，落地之后再爬山越岭、适应复杂的地形 。

这是变形金刚，它本来是一个多面体，没有手，没有脚。但是我们可以通过变形，把它变出手或脚出来。它可以滚，也可以用手脚去攀爬。

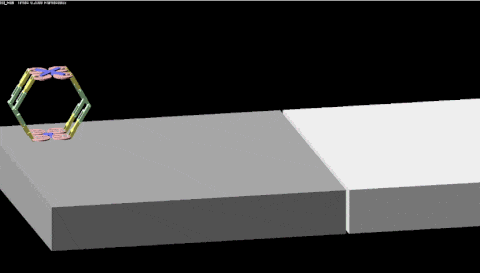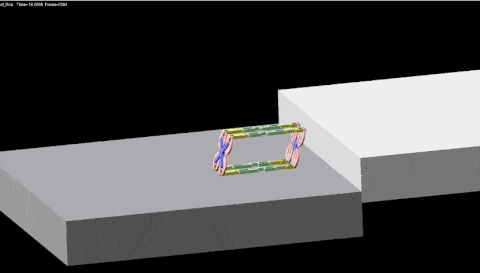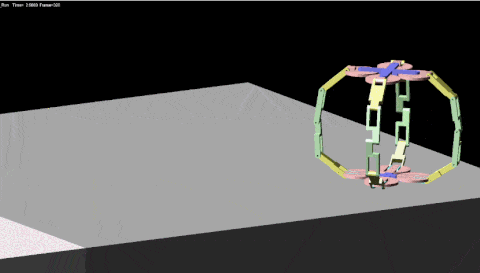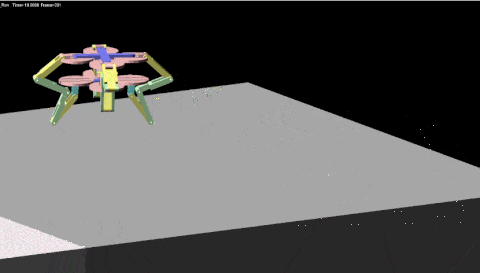这是我们目前正在做的另外一款变形金刚。变形金刚一般是把汽车变成汽车人，我们这个要复杂得多，有很多复杂的多模块组合。

除了平面几何、立体几何、拓扑几何，我们还研究了更为复杂的高维几何。

我们的物理世界是三维空间，用X、Y和Z三个笛卡尔坐标系就可以表达。但是爱因斯坦发现，实际上我们的世界不是三维空间，而是四维时空。像现在也有一些著名的几何学家、数学家，比如哈佛大学著名的华人教授丘成桐，他就在研究十一维的几何空间——他认为宇宙可能有十一个维度。

我的研究借鉴了高维几何——专门有高维几何这个学科。我一直认为数学好像远远领先于我们其他的学科，包括机器人、物理和化学。爱因斯坦在研究相对论的时候，他发现还没有很好的数学工具能描述四维时空，才去寻找四维几何学。实际上，几何学家早已经把非欧几何、四维几何准备好了。后来爱因斯坦掌握四维几何之后，就很快解决了相对论的问题。

这是我们做的一款非常玄妙的机器人，它起自于四维空间，叫双多棱柱。大家看到，它里面是个小的三棱柱，外面是个大的三棱柱。在运动过程中，里面的三棱柱可以伸出来把外面的三棱柱吞掉，外面变成里面，里面变成外面。非常有趣，也非常玄妙。

其实四维空间很重要的特性，就是 内外不分，内外一体 。

曾经有一位气功师张宝胜，有段时间非常有名，他声称可以把一个封闭瓶子里面的药片抖出来——这在三维空间里显然做不到，你除非把瓶子破坏掉。我们后来知道，这位先生是在变魔术。

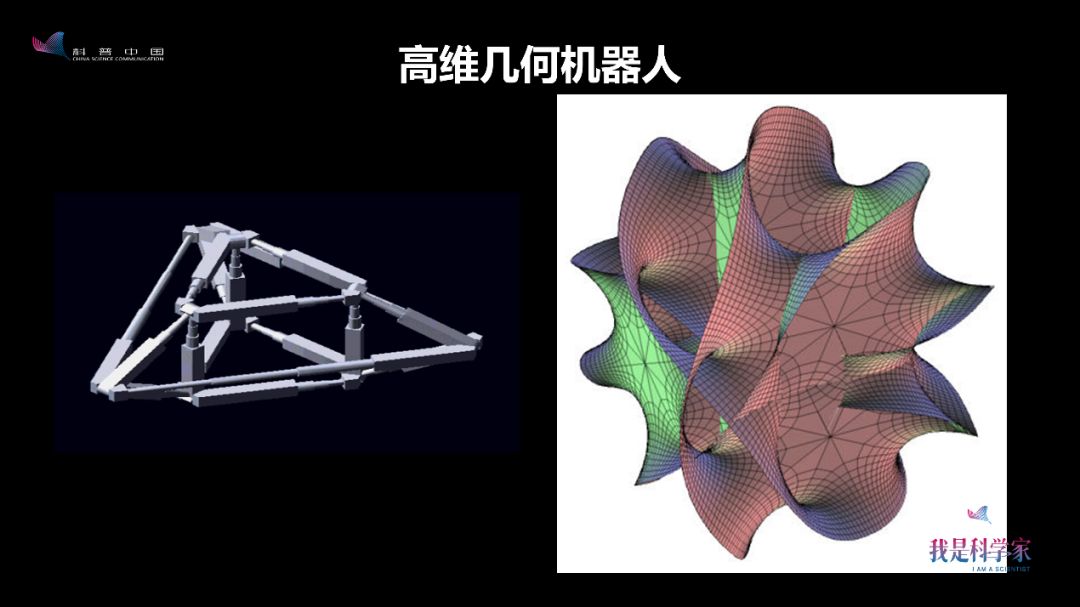实际上，四维空间的几何学真的有这种特性，比如说克莱因瓶，它真的是内外相通的。

我们团队正在进行一项更为复杂的工作，我把它叫做“超（机器）人”，用术语描述是“ 极端地形可重构多模式机器人 ”。

这是仿真录像（左图）和第一代实验样机（图右）。它的外形是多面体，可以近似球形——灵活，有全向移动能力，但不是很容易控制；也可以变成履带式——滚动行走，适应比较松软、崎岖的地形；也可以变成轮子——快速滚动。此外，在硬路面上（如高速公路），它还可以变出腿和脚去攀爬。

它有一个很独特的特性：可以折叠起来，堆在一起——很适合隐蔽、隐藏或者运输、投掷的工作。

这样，它就具备了 内在变拓扑、外部变形态 的特点。我希望用它来克服极端复杂的地形：需要快的时候就变成轮子或球形，需要跨越松软地形就变成履带或蛇形，需要攀爬台阶、壕沟、垂直墙等离散障碍就变出腿脚。

从提出几何机器人的概念到今天，我做了有十五、六年的研究。不断有人问我：你提的这个几何机器人，有什么用？

我也经常开玩笑回答——

几何学的创始人是古希腊伟大的哲学家、数学家欧几里得，他写了一本《几何原本》，在柏拉图的几何学园里来教几何学。

有一天，一个年轻人问欧几里得：我跟你学几何学，有什么用？

欧几里得就对站在他旁边的学生说：给这个小伙子三个硬币，让他走吧，他想从几何学里面学到实际的利益。

对此，我的理解是：柏拉图、欧几里得这些伟大的数学家、哲学家、科学家，他们很不希望自己的学问被看作是实用的、技术性的技巧。但是我们知道，除了古希腊之外，其他文明古国（古印度、古巴比伦、古埃及，包括古中国）实际上都把几何学作为测地术——用来丈量土地、盖房子。

其实几何学是非常有用的学问，古希腊的哲学家、数学家他们试图用它来研究宇宙的结构，探索神是怎么创建宇宙的。当时柏拉图就提出来：宇宙是由五个正多面体（正四面体、正六面体、正八面体、正十二面体和正二十面体）构成的——多面体有很多，但正多面体只有这五种。他认为，正四面体代表火，正六面体代表土，正八面体代表空气，正二十面体代表水；后来他的学生提出来，正十二面体代表上帝的一种元素“以太”。

我们做的几何机器人，它具有无用的一面，也确实有实用的一面。我在实用方面的探索，是希望把它 作为探索极端地形的机器人 。

这是2008年汶川地震的一张照片，当时我正在德国做访问学者。其实本来蜀地就没有什么路，山很陡峭——“蜀道之难，难于上青天”。地震把仅有的路面严重破坏了，所以地面的救援车辆根本过不去。天气很恶劣，地形很复杂，直升机也不敢降落，就只能靠士兵攀爬。士兵需要背很多很重的救援物资，速度很慢，也很危险——真的让人很揪心。

当时我在德国，远水解不了近渴，也没有办法。但是我给坦克装甲车研究所的工程师打电话：装甲突击车那么厉害，能不能过这种地形？很遗憾，装甲突击车也过不去。

于是我就想， 能不能做一款机器人，它能够在这种复杂地形下通行自如，进行抢险救援 ？

陆军在2016年办了一个仿生机器人的挑战赛，邀请了国内做仿生机器人比较强的团队。比赛现场有好几个仿美国大狗的机器人，而我们的铁马多足机器人有16条腿。

我们在一个山区里面比赛，这是当时的场景。铁马多足机器人跟大狗机器人采用了截然不同的设计原理，它每一只马腿都由若干层的网格叠加，很复杂，也是我几何机器人的一个延伸。最后，我们拿到了山地赛总分第一名，在载重和速度方面都超过了美国的大狗机器人。

很多人可能会奇怪：机器人是很典型的高科技，为什么又在做艺术？

我是这样思考的：高科技往往很快就会被取代，比如手机，可能两三个月就换代了，难以持久。但艺术是永恒的，比如李白的诗、齐白石的画，可能有人类存在，艺术就会不断地存在下去。那 怎么在瞬态变化、日新月异的高科技之中，探索永恒不变的元素 ？

这也是引起我关于“艺术跟科技融合”探索的动机。

实际上，我主要受到这两个人的启发：塞尚和达·芬奇。

塞尚，西方把他称为“现代艺术之父”和“新艺术之父”，他开创了包括立体主义、抽象主义等等现代艺术的画风。他认为，圆柱、圆球和圆锥这些抽象的几何元素更适合表达自然，更接近自然的本质。我跟塞尚学了一点点的皮毛，所以做出了圆柱形、圆球形和锥体的机器人。

另外，也受到了达·芬奇很深刻的影响。达·芬奇不仅是伟大的画家，同时也是一位伟大的科学家——很多巧妙的装置都是由他最初设计的。我从达·芬奇绘画里得到最大的灵感是，一种运动的艺术。其实我最开始看《蒙娜丽莎》的时候，觉得好像也没有很漂亮；但后来就越看就越入迷。我逐渐感觉到，达·芬奇的艺术造诣可能不是形态的、几何学的漂亮，而是一种巧妙、精巧又玄妙的运动的艺术。

我也创造了一些具有运动艺术的机器人作品，比如雪花机器人，它是一个比较复杂的多边形机器人。

我对流行歌曲不是很感冒。但当时听到萨顶顶唱这首歌的时候，就很有感觉：思绪像飘扬的雪花，落在地面上，变成自由行走的花。我就想，是不是真的可以做一枝可以行走的花？

后来我就做出了可以行走的雪花，当然是很抽象的雪花的造型。我也请一个舞蹈家作为舞蹈老师，排了一个雪花机器人的舞蹈，并且请了小演员表演群舞。

机器人是一种智能的生命，它跟传统的机器都不一样。它有智能，有自主感知运动的能力，有可能跟人类是一样的。那将来，机器人怎么跟人类去共融相处？所以我希望尝试“ 人机融合 ”。

我们也尝试借鉴了艺术领域的一些流派和风格，来做一些机器人艺术作品的创作。

比如，这是我和康奈尔大学教授、中央美院客座教授陈小文合作创作的撞南墙圆柱机器人。得知我的机器人是圆柱体，陈老师提议：能不能让它去撞南墙？结果做出来的这款机器人就不断地撞墙——撞完墙，退回来，再撞——我觉得有点“行为主义”的味道。

这是一个滑行四边形机器人，其实在仿蛇形；但形是一条曲线，不是蛇形——神似形不似。

这个双三角锥机器人，以数学图阵里一个很著名的问题命名，叫Random Working。它有一个非常有意思的特性：可以在地面上随机行走。

它像一个醉汉——一会清醒，一会糊涂，有时候第一步知道往哪里走，结果第二步就不知道了。

这个鼎是我的镇宅之宝。我跟中科院自然科学史研究所张柏春所长非常熟，也认识一位用现代技术做鼎的苏荣誉老师。所以有一次我们三人聊天，我就请两位老师指导一下。

苏老师很感兴趣，说这个是行鼎；但是古鼎专家也没有搞清楚到底什么是行鼎，因为出土文物很少。他说，这可能是世界上第一台真正能走的鼎，干脆我给起个名字叫“姚氏行鼎”。但是张老师就质疑：鼎本来是静物，一言九鼎，不能动——这晃来晃去算怎么回事？

张老师的话困扰了我很长时间，让我好几年都不敢往外推——我做的装置不被科技史专家认可，大概也不太好办。后来我想，牵强一点，干脆让它“ 动如脱兔，静如处子 ”——平常让它不动，但每隔半个小时让它出来转一圈。

前段时间，我在798的成当代艺术中心举办了一个几何机器人的科学艺术展，上图是当时的一个展品。这双鞋子实际上是个机器人，也可能是 世界上最简单的机器人 ，只有两只脚——我把它简化到只有两只脚，连身子都没有了。我做了机器人的骨架，后来陈老师帮它穿了两只鞋，中央美院的几个研究生也参与了创作。展出时只有一个电机，只用了一个马达，很好地体现了极简主义的风格。

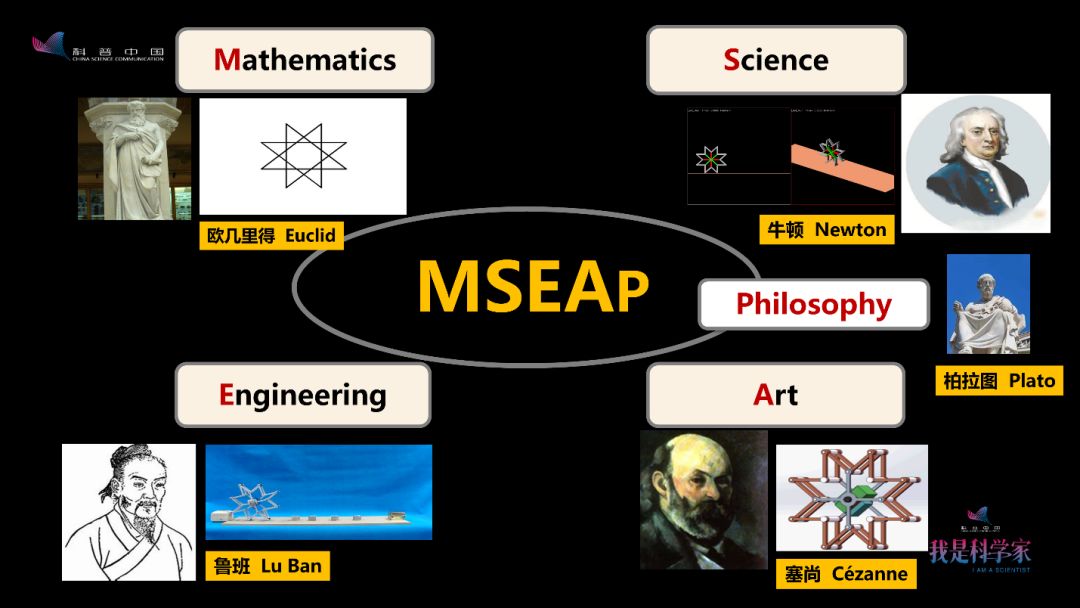我提出了MSEAP的理念，五个英文字母分别代表数学（Mathematics）、科学（Science）、工程（Engineering）、艺术（Art）和哲学（Philosophy）。静态的几何图形，通过力学（代表科学），可以变成可动的物理装置（即机器人），再通过工程的设计、制造、加工、检测，可以变成实用的产品。我还要通过艺术的设计，使它更美妙，更符合美学的视角。另外，也希望融入哲学思想，使它具有普世性。整个过程，我把它概括为 数学的严谨思维、科学的创新精神、工程的实践能力、艺术的美学视角还有哲学的普世情怀 。

几何机器人有有用的一面，可以装摄像头，可以侦查探测，可以运载、运输，也可以放枪、放炮。作为超级金刚、作为武器，它有强大的力量，可以救人，也可以杀人。

最初柏拉图、欧几里得这些古希腊伟大的数学家、哲学家，他们用几何学来研究宇宙的结构和秩序；牛顿完全继承了他们的衣钵，提出了万有引力定律，认为万物包括宇宙天体要有力来推动运动——这样的话，整个宇宙其实变成了一部机器。在他们的基础上，我稍微引申了一点点，把机器人引入到几何学里面。

机器（包括汽车、飞机）是人设计和制造的，但是人和动物是进化来的，这是两个不同的技术路线。那么，机器人将往哪里走？它是人造的，但又有智能，可能比人类更聪明。孩子被父母生出来之后，就可能不受父母控制了——机器人也可能如此。目前来看，机器人的体力已经超过了人，存储、计算能力也超过了人（比如AlphaGo），实际上逻辑分析能力可能也已经远远超过人了。

我的看法是，机器人超过人是必然的，可能指日可待。这样的话可能会引起很多人的忧虑和思考：如果机器人真的比我们还厉害、强大，它会不会对人类不利，甚至毁灭人类？

我很喜欢看武侠小说，一直很喜欢“强大的武功和力量掌握在正义之人手中”的剧情。比如降龙十八掌，这么强大的武功掌握在萧峰手中，我们不会很担心，但是如果掌握在星宿老怪手中，世界可能就会一团糟——我很希望强大的力量能够掌握在正义的人手中。

我也非常喜欢《西游记》，这段时间我一直在研究它。大家都知道观音菩萨是慈善和美丽的化身，但其实她也有非常强大的力量。孙悟空和观音菩萨之间，曾经有过这么一段故事：观音菩萨让孙悟空拿她的玉净瓶去对付红孩儿。孙悟空就去抓，但根本抓不动，他就很不服气，为什么菩萨轻轻一拎就能它拎起来了？菩萨说，你神通广大，但只有担山之力，没有架海之力，玉净瓶里装的是五湖四海的水，你的力量还差很远。

我希望我的机器人将来能成为菩萨一样的美丽的强者， 造福人类，维护世界和平 。

谢谢大家。

演讲嘉宾姚燕安：《我想让几何机器人摸爬滚打，成为美丽的强者造福人类》

作者：姚燕安

编辑：麦芽杨、凝音

在“我是科学家iScientist”后台回复“演讲”，或者点击菜单栏“演讲”，即可看到更多科学家演讲。