[科普中国]-黎曼，除了他的猜想，还有哪些不为人知的故事？

作者： 伊随

编辑：Yuki

随着菲尔兹和阿贝尔奖双料得主迈克尔·阿蒂亚爵士宣称自己证明了黎曼猜想，黎曼的名字和他的世纪猜想再次回到公众的讨论之中。然而，黎曼，除了他的猜想，还有一些故事也是非常值得我们去了解的。

（黎曼，拍摄于1863年。图片来源：sil.si）

对于一个非数学专业的人而言，要问他所听说过的伟大的数学家有哪些？我想很少会有人提到黎曼的名字。但是，如果换一种方式问他，是否听过发明微积分的牛顿和创立相对论的爱因斯坦，我想大多数人应该都会有所耳闻。

殊不知，当今在物理、化学、经济学都密切相关的微积分计算和高大上的相对论，都离不开这个不怎么为人所知的伟大数学家——黎曼。

黎曼几何

广义相对论的数学基础

如果说爱因斯坦的成功也是站在了巨人的肩膀之上，那么这个巨人可能就包括黎曼。

在一个世纪前，爱因斯坦在计算广义相对论时，有些数学方面的难题难以解决。爱因斯坦在数学家朋友的帮助下， 发现黎曼几何的理论体系完美符合他的广义相对论的问题情境，从而利用黎曼几何学构建了广义相对论方程 。

那么何为黎曼几何呢？

我们最为熟悉的几何当然就是从中小学就开始接触的欧式几何，整个欧式几何从我们人类的经验和直觉出发，建立在五大几何公理体系之上（比如过两点有且只有一条直线，线段可以无限延长等等）。而第五条公理，也就是平行公理，引起了众多数学家的关注。

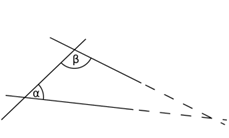
（第五公理。图片来源：Wikimedia Commons）

高斯、罗巴切夫斯基等都认为平行公理同其他四条公理相较而言，显得有些奇怪，无法用其他的公理来证明对或错。随后，罗巴切夫斯基重新定义了一种新的平行公理代替了欧几里得平行公理，建立了罗氏几何（也叫双曲几何）。

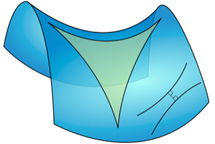
（罗氏几何。图片来源：Wikimedia Commons）

继罗氏几何后，德国数学家黎曼在1854年又提出了既不是欧氏几何也不是罗氏几何的新的非欧几何——黎曼几何（也称椭圆几何） [1-3] 。黎曼几何中规定，在同一平面内任何两条直线都有交点，所以在黎曼几何学中不存在我们所熟知的平行线。并且黎曼几何还约定直线有界但能无限延长。

看到这里，是不是发现黎曼几何的一些特征已经与广义相对论的模型相似？ [7,8] 没错，它就是广义相对论的数学基础！！ 大名鼎鼎的爱因斯坦的大名鼎鼎的广义相对论就好像是黎曼几何的一道应用题。

（广义相对论。图片来源：Wikimedia Commons）

黎曼积分

微积分首次具有了严谨精确的定义

我们都熟知微积分是牛顿和莱布尼茨发明的，我们今天利用微积分计算一块区域的面积、计算发动机的功率、计算空气动力、计算磁场强度等等，无时无处不渗透着微积分。然而，我们所学到的微积分与牛顿和莱布尼茨在发明微积分的时期是完全不同的。

牛顿采用了流数法，莱布尼茨采用了数列阶差，而且微积分的记号形式也更为简洁，这两种方法都可以得到正确的积分结果，但是都缺少严谨的数学逻辑基础 [4,5,10] 。 正是黎曼在柯西等一些分析学数学大师的研究基础上，建立严谨的微积分理论基础。

时至今日，黎曼积分仍然是科学研究中用到的最广的一套微积分理论。直到数学家发现一些奇异的函数难以用黎曼积分来求解，才相继出现了黎曼－斯蒂尔杰斯积分和勒贝格积分 [6,10] 。

（曲线围绕图形的面积。图片来源：Wikimedia Commons）

哥廷根大学

黎曼的母校，近代欧洲数学的摇篮

哥廷根是一个只有十几万人口的德国小镇。而哥廷根大学，一个小众的学校名字，相较于牛津、剑桥、哈佛、耶鲁来说，可能几乎没有什么人听说过，就像没有多少人听说过黎曼的名字一样。但是，历史无法掩盖它昔日耀眼夺目的光芒。那是一个风云际会、百花齐放的哥廷根时代。 [9]

它的辉煌始于数学奇才高斯，在此之后，黎曼、狄利克雷、雅可比和菲利克斯·克莱因相继涌现，众星云集，在数学的众多领域，包括代数、几何和分析领域做出了巨大的贡献。一直到大卫·希尔伯特，德国哥廷根数学学派进入了全盛时期。

除此之外，哥廷根大学在物理学领域也毫不逊色，著名的物理学家包括普朗克、赫兹、海德堡、费米、泡利和奥本海默等等。据统计，前后共有46名诺贝尔奖得主，或在此读书或教学。恐怕世界上很难再找到一个城市，能有如此伟大的学术荣耀。

数学猜想

那些被证实和没有被证实的

数学猜想

数学家常常以猜想的形式提出问题，这些猜想可能对人类科技的发展没有直接的影响，但是在证实猜想的过程中，所迸发出的新方法和新思路却给数学的科学带了重要的作用。也许，这也算是数学猜想神秘而迷人的一个方面吧。

最有名的数学猜想恐怕非哥巴赫猜想莫属了，除此之外还有四色猜想和费马猜想。其中费马猜想于1994年由英国数学家安德鲁怀尔斯完成证明，因此不再称为猜想，而称为费马大定理。四色猜想由美国数学家阿佩尔和哈肯借助计算机完成，从而被称为四色定理。 哥德巴赫猜想至今还没有完成证明，目前最好的结果还是我国数学家陈景润取得的。

除了这三个之外，最著名的要数德国数学家大卫·希尔伯特的世纪之问了。他在19世纪和20世纪之交的1900年世界数学家大会上提出了23个数学问题，这被誉为当时数学的顶峰。黎曼猜想便是其中之一，时至今日，绝大多数已经经过无数数学家前赴后继的研究得以证实。

每个攻克这些数学难题的人都被看作是学术造诣的巅峰，载入史册。那些没有被证明的猜想，依然像珠穆朗玛峰一样矗立在远方，激励着无数的勇敢者去攀登去征服。

也许，数学家确实不像其他领域的大师和那样能够吸引更多的眼球和聚光灯，但是不可否认， 数学家依然是人类智慧星空上闪亮的星，他们发出的光芒虽然从来不是最耀眼的，但是往往每次都指引着人类科学前进的方向。

作者名片

排版：小爽

题图来源： tech.sina

参考文献：

[1]https://en.wikipedia.org/wiki/Bernhard_Riemann

[2]https://en.wikipedia.org/wiki/Riemann_integral

[3]https://en.wikipedia.org/wiki/Riemannian_geometry

[4] 《Calculus》,Gilbert Strang

[5] 《微积分概念发展史》, Carl B.Boyer

[6] 《实变函数论》, 周民强

[7] 《微分几何入门与广义相对论》, 梁灿彬、周彬

[8]https://en.wikipedia.org/wiki/Hyperbolic_geometry

[9]https://en.wikipedia.org/wiki/G%C3%B6ttingen

[10] 《微积分的历程》, 邓纳姆