[科普中国]-你知道古希腊三大几何问题吗？

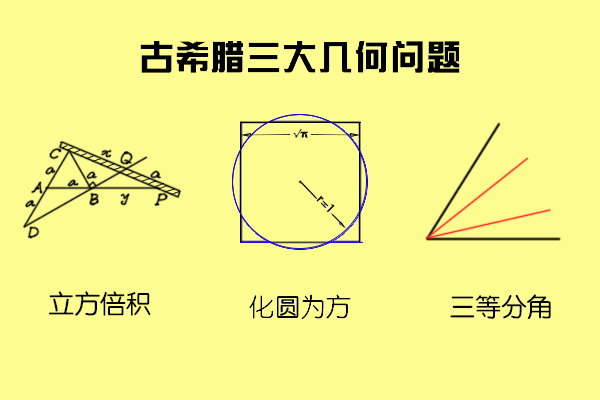
圆规和直尺是非常重要的作图工具，仅使用无刻度的直尺和圆规作图的方法叫尺规作图。尺规作图来源于古希腊的数学课题，利用尺规作图方法可以作出很多基本图形，但却不能解决所有问题。被称为“古希腊三大几何问题”的三等分角问题、倍立方问题、化圆为方问题，便无法用尺规作图的方法轻松解决。

取一个任意角，作出其三等分线，即为三等分角问题。在尺规作图中，将任意角二等分、四等分或八等分是容易解决的。画一个任意角，以顶点O为圆心，取任意长度为半径画弧，任意角的两条边与弧相交于A、B两点。再分别以A、B两点为圆心，取相同且大于A、B间距一半的长度为半径画弧,两段弧相交于点C。连接O、C两点，直线OC即把这个任意角分成了二等分，如此反复下去即可得到四等分、八等分、十六等分等。偶数等分易得，但三等分却不可得。

取一个任意大小的立方体,作出体积是它两倍的立方体，即为倍立方问题。取一个任意大小的圆，作出面积和它相等的一个正方形，即为化圆为方问题。解析几何的出现，为数学家提供了新的研究方法，最终证明了这三个几何问题只利用尺规作图不可解。

坐标计算的带入，让几何问题转变成为代数问题。直线可视为一次方程，圆相当于二次方程，尺规作图也就可归纳为一个二次方程组。数学家在对代数方程和抽象代数进行一系列研究后发现，从单位长度出发，尺规作图可以作出的长度,恰好是自然数通过有限次四则运算和开平方能得到的所有数。

在三等分角问题中，若尺规作图时假设给定了一个单位长度,那么作出任意一个确定的角，就相当于作出了这个角的正弦值。比如，通过尺规作图可作出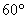的角，是因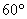角的正弦值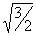可通过有限次四则运算和开平方得到。而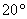角——也就是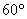角的三等分角，正弦值却无法通过有限次四则运算开平方得到，也就是说无法只用尺规作出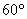角的三等分。由此可知，三等分角问题不可解。

在倍立方问题中，假设将这个任意立方体的棱长作为单位长度,那么体积是它两倍的立方体的棱长为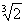，此数不能通过有限次四则运算和开平方得到。由此可知，倍立方问题不可解。

在化圆为方问题中，假设任意圆的半径为1个单位长度,其面积为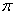，那么面积相同的圆的边长即为。德国数学家林德曼早在1882年就证明了π是一个超越数。所谓超越数是指不满足系数不全为零的整系数多项式方程的数，也就是说超越数不能通过有限次四则运算和开平方得到。由此可知，化圆为方问题也不可解。

然而人们在研究这些问题时发现，只要更改了古希腊尺规作图的一点条件，这三大问题就不那么困难了。阿基米德曾在直尺上做了一个记号，使得直尺实际具备了刻度功能，解决了三等分角的问题。

即使这三大问题被代数证明仅用尺规作图不可能解决，但是这并不妨碍我们去尝试研究。在研究三大几何问题的过程中，数学家开创了对圆锥曲线的研究、发现了尺规作图的判别准则等，这些问题要比三大几何难题本身更有意义。

本文由中国人民大学附属中学第二分校一级教师秦薇进行科学性把关。

本作品为“科普中国-科学原理一点通”原创，转载时务请注明出处。