[科普中国]-神奇的运动悖论——浅析芝诺悖论

空中飞行的箭其实是静止的？奔跑的人无论再快也永远追不上前面的乌龟？这样的说法你能接受吗？射出去的箭为什么不动呢？人的运动速度怎么可能追不到乌龟呢？

这些便是古希腊数学家芝诺提出的一系列关于运动的哲学矛盾论述——芝诺悖论。据说，芝诺是一个勤奋刻苦、自学成才的乡村少年，为了捍卫老师巴门尼德的学说，他提出了许多悖论以表明运动的不可能性。其中，最著名的悖论有四个，今天我们就为大家揭开它们的神秘面纱。

飞矢不动悖论

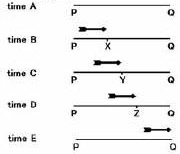
著名学者赵敦华先生在《西方哲学简史》中对这个悖论表述如下:飞矢在一段时间里通过一段路程, 这一段时间可被分成无数时刻；在每一个时刻，箭矢都占据着一个位置，因此是静止不动的；就是说，它停驻在这段路程的各个不同位置上，而不是从一个位置飞至另一个位置。

箭射了出去，在视觉上当然是运动着的，怎么可能是静止的呢？其实，芝诺刻意忽略了时间空间的连续性，所强调的是不能忽略运动中的静止。

阿基里斯追乌龟悖论

阿基里斯是希腊神话中最善跑的英雄，然而在芝诺悖论中，只要乌龟先起跑，阿基里斯便永远追不上乌龟。因为阿基里斯只能追到乌龟曾经到达的地方，那一瞬间乌龟又总是又向前移动了，于是产生了新的起点，阿基里斯继续追，而乌龟也在前进，就会又一次产生新的起点。阿基里斯再去追新的起点，乌龟还会继续向前移动。这样，乌龟会制造出无穷个起点，阿基里斯永远都追不到前面的乌龟。

听起来是不是非常不可思议？那么如何破解这个悖论呢？亚里士多德对阿基里斯追乌龟悖论的解释是：当追赶者与被追者之间的距离越来越小时，追赶所需的时间也越来越小。他认为，无限个越来越小的数加起来的和是有限的，所以不用担心，阿基里斯是可以在有限的时间追上乌龟的。

游行队伍悖论

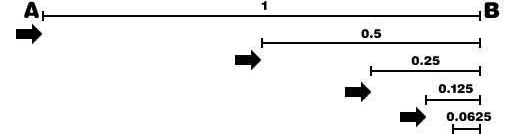
假设在一瞬间，相对于观众席A，列队B、C将分别向右和左移动一个距离单位，B、C两个列队开始移动，那么相对于观众席A，B和C分别向右和左各移动了一个距离单位，而此时，对B而言，C移动了两个距离单位。

事实上，假定一个物体以相同的速度通过一个移动物体和一个同样大小的静止物体时，所需时间相等，而这个假定是违反自然规律的。人们曾经试图从哲学的角度或是逻辑的角度对该悖论进行反驳或破解，但至今仍有争论。

二分法

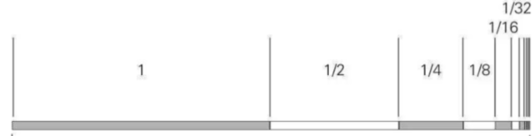
芝诺认为，一个人从A点走到B点，要先走完路程的1/2，再走完剩下总路程的1/2，再走完剩下的1/2，如此循环下去，永远不能到终点。

其实，芝诺在偷换概念。有限的距离和有限的时间都是无限可分的，但总长仍是有限的；无限可分的有限距离和有限时间并不意味着它们变成无限本身，所以在有限时间内是可以通过有限长度的。

芝诺悖论是非常复杂的涉及哲学、数学等学科的问题，揭示的矛盾是深刻而多层面的。他的论证虽然有缺陷, 但他是欧洲哲学史上第一个使用逻辑推理揭示矛盾的哲学家，在客观上却触及了辩证法的核心，因此，芝诺悖论从诞生之日起就持续引发着学者们的争论。

本作品为“科普中国-科学原理一点通”原创，转载时务请注明出处。