[科普中国]-怎样计算用淘汰制进行的比赛场数

淘汰赛，就是将比赛分为连续的几个轮次，每一轮都有几组两队之间的比赛，败者被淘汰，胜者进入下一轮继续分组进行比赛。最后一轮通常被称为决赛，决赛中的胜者即为冠军。这种赛制下，参赛者必须赢得每一场对战才能够获得最终的胜利，这也被称为单败淘汰制。单淘汰制也是最常见的淘汰赛制。

除单淘汰制外，淘汰赛制还有双败淘汰制和三败淘汰制。双败淘汰制在输给两个对手之后才会被淘汰；同样地，三败淘汰制在输给三个对手后会被淘汰。在运动竞赛中，淘汰赛的赛制在很多类别的体育项目中被广泛应用。

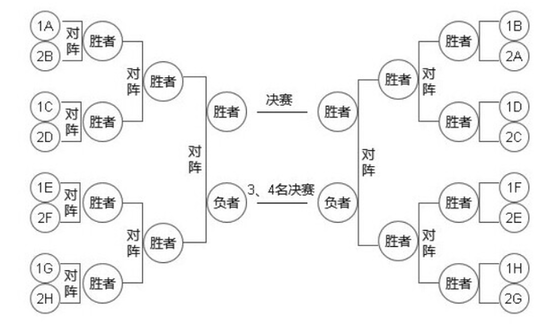
本文所要说的计算比赛场数将以单败淘汰制为例。由于淘汰赛需要每两个参赛者进行一次比赛，直到最后选出两名参赛者进行决赛，因此，在保证每一场比赛都有对战的情况下，参赛者的数量应为2的整数次幂，即2（21）、4（22）、8（23）、16（24）、32（25）、64（26）等。这样就只需要将每两位参赛者编成一组，各自比赛逐步淘汰，在这种理想的情况下，比赛轮次就是2的整数次幂。那么比赛的场次会是多少呢？

我们以16名参赛者为例，首先要进行8场初赛决出8名可以参与下一轮比赛的参赛者，接下来需要4场、2场以及一场决赛才可以决出一名冠军。也就是说16名参赛者参与的淘汰赛需要进行8+4+2+1=15=16-1=24-1场比赛。同理，32名参赛者需要进行的比赛场次为16+8+4+2+1=15=31=25-1场比赛……也就是说对于位参赛者而言，淘汰赛的比赛场次为2n-1场。

但是在实际情况中，参与比赛的报名者数量不会刚好是2n，这时比赛过程中就会出现轮空的情况。假如将选定的参赛者在比赛的中后阶段进行轮空，此时，非轮空的参赛者水平趋于一致，轮空与非轮空参赛者之间存在不公平的情况。而比赛最重要的原则，就是保证获胜的公平性，因此，通常将轮空这一环节放置于淘汰赛的第一轮。我们假设有47名参赛者，为了保证除第一轮以外的后边的轮次都不会产生轮空，第一轮之后剩下的参赛者数量将为距离47最近的2的整数次幂，也就是32。第一轮将会淘汰47-32=15名参赛者，也就是需要进行15场比赛，47-15×2=17名参赛者轮空。此时，需要进行的比赛场次一共为15+25-1=46，刚好为47-1。

也就是说，单败淘汰制的比赛，每一场都会淘汰一名参赛者，为了决出n名参赛者之中的冠军，一共需要进行n-1场比赛，淘汰掉非冠军的n-1名参赛者。

为了保证更高的公平性，淘汰赛通常会设置种子选手或排名制度，以免实力强劲的参赛者过早参加比赛，实力最强的参赛者通常会在决赛相遇。这样的设定在一定程度上保证了比赛赛制的公平性。

本作品为“科普中国-科学原理一点通”原创，转载时务请注明出处。