[科普中国]-从七桥问题初探拓扑学思维

柯尼斯堡七桥问题是图论中的著名问题，也是复杂网络的源头理论。

18世纪初普鲁士的哥尼斯堡，有一条河穿过，河上有两个小岛，为方便同行，人们在河上修建了七座桥，把两个岛与河岸联系起来。有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。

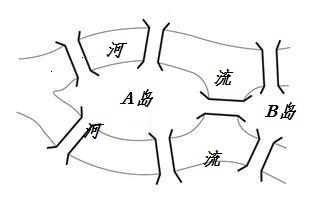
问题提出后，很多人对此很感兴趣，纷纷进行试验，但在相当长的时间里，始终未能解决。而利用普通数学知识，每座桥均走一次，那这七座桥所有的走法一共有5040种，而这么多情况，要一一试验，这将会是很大的工作量。但怎么才能找到成功走过每座桥而不重复的路线呢？于是大家去请教年轻的数学家欧拉。但欧拉当时也没有意识到这是一个数学问题，他也想过使用列举法，列举所有可能的路线，但是他认为这样没有意义，对解决之后同类问题没有参考意义。于是，便在1936年提出将其转化为一个抽象的数学图形模型，将其转化为一笔画问题，这种思维模式就是抽象与符号处理的方法。

欧拉在研究一段时间之后，将两个对岸与两个小岛这四块陆地抽象为四个点，将通过河流连接四地的七座桥抽象为七个线段，将路程这个因素与其他跟过桥无关的要素全部舍弃，于是就将上文的地图抽象为下图：

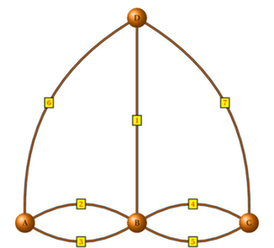
问题至此便被转化为了一笔画问题。我们将四地分别编号为A、B、C、D，将七座桥用数字1—7来表示。从图中可以看出，A、B、C、D四个点所连接的线段数都为奇数，我们就只需以点A为起点分析，就能够同理得出以其他三点为起点的情况。假设从A点出发，如果首先通过2号桥出发，最后通过3号桥返回，那么在每座桥只允许通过一次的情况下将永远不会经过6号桥。因此A点不能作为起点，同理，B、C、D三点也无法作为起点。因此七桥问题无解。

欧拉通过对七桥问题的研究，不仅圆满地回答了哥尼斯堡居民提出的问题，而且得到并证明了更为广泛的有关一笔画的三条结论，人们通常称之为欧拉定理。对于一个连通图，通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。欧拉在解答问题的同时，开创了数学的一个新的分支——图论与几何拓扑，也由此展开了数学史上的新历程。

本作品为“科普中国-科学原理一点通”原创，转载时务请注明出处。