[科普中国]-历法中的数学

数学自古至今时时充斥于我们生活的角角落落，并对我们的生产和生活产生重大影响。天文中的历法同样也蕴含着数学的玄机。

公历中的闰法

我们现在使用的历法为国际通用的公历，又称阳历。公历有平年和闰年之分，平年有365天，其中二月有28天，闰年366天，其中二月有29天。公历中的闰法对闰年是这样规定的“四年一闰，百年少一闰，四百年加一闰”。为什么公历中要安排复杂的闰法呢？

其实这是由地球围绕太阳公转决定的。我们知道，地球绕太阳公转一圈的时间为365天5时48分46秒，而平年仅有365天，剩余的5时48分46秒是二者之间的误差，需要折算成天数，通过加闰的办法，即在二月份加一天，就可将积累的误差吸收掉。以天为单位，用分数的形式表现这个误差为：

a＝5/24＋48/24×60＋46/24×60×60=10463/43200≈0.2421991。

从这个分数算式可以看出，在43200年中，需要安排10463个闰年，而消除误差最好是均匀加闰，但却不便操作和记忆。如果我们用连分数即可提供方便记忆的闰法。

运用辗转相除法很容易得到误差a的连分数表示式为：a＝10463/43200＝1/4＋1/7＋1/1＋1/3＋1/5＋1/64。

由连续式可以看出，第一个渐进分数a1=1/4=0.25，说明每隔四年就应该加一天，这就是所谓的“四年加一闰”。由于它是个近似值，而不是精确值，因此还需要修正。第三个渐进分数为a3＝1/4＋1/7＋1/1＝8/33≈0.2424242……说明每隔33年就需要加8天，每隔99年需加24天就比较与实际接近。因此100年（与99近似）中应加24天，而不是加25天。这就是“百年少一闰”。如果始终按每100年加24天，那么43200年就应加432x24=10368（天）。

由a＝10463/43200可以知道，经过43200年，就应该加10463天，这就比实际少加了95天，所以，闰法又有了“四百年加一闰”的修正。但是，按照这种规定，就可以算出43200年共加了10463天，比实际又多增加了13天，这又意味着每隔3323年就又多加了一天。而这些还需做进一步的修正。

从以上的介绍可以看出，现在使用的历法，其精确度是相当高的，但仍需要进行随时修正，而这一切，均与数学密不可分。

农历中的“十九年七闰”

中国从古代一直沿用的历法为农历，它是由月球绕地球公转决定的。农历中的一个月，称为“朔望月”，约为29.5306天。由于地球绕太阳公转一周需要365.2422天，因此在一个公历年中应该设置“农历月”的个数为：

365.2422/29.5306＝12＋10.8750/29.5306

从这个算式可以看出，如果每个农历年均设有12个月，那么就会产生a=10.8750/29.5306=0.3682621的误差。要想把这种积累的误差消除掉，就必须在农历年份中增加一个月，这个月就是闰月，这个年就称为闰年。那么，怎样增插闰月呢？这就需要先求出a的连分数表示式：

a＝1/2＋1/1＋1/2＋1/1＋1/1＋1/16＋1/1＋1/5＋1/2＋1/6＋1/2＋1/2

从上面的表示式可以看出，它的前六个逐次渐近分数依次为：a1＝1/2≈0.5，a2＝1/3≈0.3333333，a3＝3/8≈0.375，a4＝4/11≈0.3636364，a5＝7/19≈0.3684211，a6＝116/315≈0.368254。由此可得，a2＜a4＜a6＜a＜a5＜a3＜a1。这表明这些渐进分数是从左、右两个方向向a的真值逼近的。

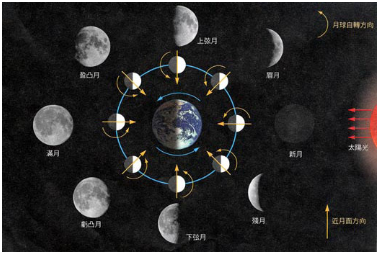
朔望月的形成

这些渐进分数所表达的实际意思是：2年1闰太多，3年1闰太少，8年3闰太多，11年4闰太少，19年7闰太多……但是其精确度却在逐渐提高。如果采用315年116闰的话，其精确度肯定会更高些，但具体制定起来难度非常大，因此，既能比较精确，又能方便制定的闰法当然要数“19年7闰”了。

与公历闰年不同的是，农历中闰年的设置不像公历那样有简单的规律。它的设置与一年中的二十四节气紧密关联，因而就会使得农历年份中有的年份没有立春，有的年份却有两个立春。事实上，我国的农民安排农耕农种，其依据是二十四节气，因此二十四节气才是真正的农历。

二十四节气

玄妙的七色表：可查出任一天是星期几

如果你想知道某一天是星期几，办法和途径是很多的，比如，可以查电脑、手机、手表、万年历等。还有一种途径或许你不太熟悉，它就是《七色表》，通过它你可以快速查出任意一天是星期几。那么，《七色表》是什么呢?

1.《七色表》的构造和使用方法

《七色表》共有五个栏目：“星期栏目”、“月份栏目”、“日期栏目”、“公元年份栏目”及由红、橙、黄、绿、青、蓝、紫七种颜色组成的“七色栏目”。

用《七色表》査找某一天是星期几的方法非常简单，举一个例子来说，你要查出1970年6月3日是星期几，首先你在“月份栏目”内找到6月份所在的横行，在“日期栏目”内找到3日所在的竖列，在“七色栏目”内二者的交汇处为“橙色”，记住这个颜色；再在“公元年份栏目”内找到1970年，往左在“七色栏目”内1970年所在的行中查到“橙色”，它在上面“星期栏目”对应的是星期三。

2.《七色表》的由来

《七色表》虽然用起来很简单，但它却似乎非常“玄不可测”，那么它是如何编制出来的呢？

我们知道，如果知道某年的1月1日是星期几，那么我们很容易算出这一年中任意一天的星期数，仅需正确算出这一天与1月1日之间相隔几天就可以了。

公元X年的元旦是星期几称为“年代号”，用N表示，其取值集合就是｛0，1，2，3，4，5，6｝，其中的0表示星期日。我们需要找到一个能够求出任意一年的年代号的公式。

假设公元1年的1月1日为星期一，即它的年代号为N1=1。根据这个假设推导出来的公式，去推算每个年的年代号，如果得出的年代号都是正确的，那么这个假设自然就是正确的。

我们知道，平年有52个星期加1天，闰年有52个星期加2天，因此有：N1＝1，N2＝2，N3＝3，N4＝4，N5＝5，N6=0，N7＝1……意思是，假如X年为平年，那么Nx+1＝NX＋1；假如X年是闰年，那么Nx+1＝NX＋1。根据公历“四年一闰，百年少一闰，四百年加一闰”的润法，即可得到Nx＝x＋〔（x－1）/4〕－﹝（x－1）/100﹞＋﹝（x－1）/400﹞。

在这个公式中，中括号内的数值均为其中分数的整数部分，这三个中括号的计算结果，即为公元1年至X年之间共出现的闰年个数。我们不难求出21世纪下列各年的年代号：

如果想知道X年y月z日是星期几，就要先求出年代号Nx。再算出从1月1日到y月z日的前一天总共有多少天，用h表示（y月z日这一天除外），在前y-1月中，它就是大月的月数乘以31（或乘以3），小月的月数乘以30（或乘以2），与2月份的28天或29天（或加上0或1）相加，再与z－1相加，最后用S＝Nx＋h除以7，得到的余数即为所要求取得星期数。

如果你认为计算总天数太复杂，那么可用“月代号法”。我们知道，如果知道一个月的1日是星期几，我们就不难推算出这一月的任意一天是星期几，因此这一年中你只要知道每个月的1日是星期几，就能推算出这一年的任意一天是星期几。这一年中的12个月代号数字，就构成了这一年的“月代号数列”，这种数列具有显著的规律性，是根据公历的大小月和闰法来确定的。下图表示的就是2010年到2014年的“月代号数列”，其中有12个粗体数字，表示的是比上年对应的同月数字多2，其他部分均多1。根据这种“月代号数列”，就可制造出《七色表》。

需要特别注意的是，公元前45年至1582年10月4日，使用的是儒略历。而现在通用的格里历，是从1582年10月15日开始的，这中间有10天是跳过来的。因此，运用《七色表》查找星期的方法仅适用于格里历。

本作品为“科普中国-科学原理一点通”原创 转载时务请注明出处