[科普中国]-维纳滤波

维纳滤波器（wiener filtering) 的本质是使估计误差（定义为期望响应与滤波器实际输出之差）均方值最小化。1

离散时间维纳滤波理论是从维纳关于连续时间信号的线性最优滤波器这个开拓性工作演变过来的。维纳滤波器的重要性在于，它为广义平稳随机信号的线性滤波提供了一个参考框架。1

基本原理维纳滤波由N.Wiener于1942年，基于最小均方误差准则下提出的最佳线性滤波方法,但是去噪的效果不太好。2

在自适应滤波中，最广泛采用的目标函数之一是均方误差（MSE），其定义为3

输出信号是由来自于阵列的信号的线性组合构成的，3

其中， 分别是输入信号和自适应滤波器系数向量。3

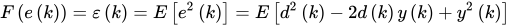
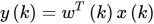
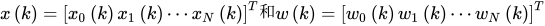
在线性组合器和FIR滤波器情形下，目标函数可以写为，3

对于具有固定系数的滤波器而言，MSE函数为，3

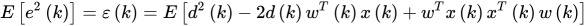
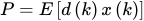
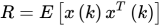
其中， 为期望信号与输入信号之间的互相关向量，且 为输入信号的相关矩阵。3

要求输入过程广义平稳1

重要特性**正交性原理，**维纳滤波器产生的误差信号（估计误差）正交于它的抽头输入信号；1

**误差信号统计表征为白噪声，**当滤波器长度与描述观测数据（即期望响应）产生的多回归模型阶数匹配时，这个条件成立。1

物理类型归入维纳滤波理论范围的滤波器结构有两种不同的物理类型：1

横向滤波器，以有限脉冲响应为特征。1

窄带波束形成器，由一组权值可调、间隔均匀的天线元素组成。1

这两种结构具有相同的特征：它们都是线性系统的实例，其输出都定义为权向量与输入向量的内积。1

本词条内容贡献者为:

尚轶伦 - 副教授 - 同济大学数学科学学院