[科普中国]-自振周期

自振周期T为结构系统按某一振型完成一次自由振动所需要的往复时间。

定义自振周期T为结构系统按某一振型完成一次自由振动所需要的往复时间。

计算公式及影响因素结构的自振周期顾名思义是反映结构的动力特性，自振周期T只与自身质量m以及刚度系数k有关，具体对单自由度就只有一个周期，而对于多自由度就有同模型中采用的自由度相同的周期个数，周期最大的为基本周期，设计用的主要参考数据。。计算公式为：

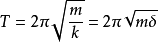(m为质量，k为刚度系数，δ为柔度系数。）

按照建筑结构荷载规范和一些参考资料， 结构基本自振周期大致为：

框架结构T=(0.12~0.15)n，其中n为楼层数；

框—剪和框—筒结构 T=(0.08~0.12)n，其中n为楼层数；

剪力墙和筒中筒结构 T=(0.04~0.06)n ，其中n为楼层数。1比如：一栋18层普通剪力墙住宅，按照上式估算 T=(0.04~0.06)X18=0.72~1.08 。

自振周期的计算是动力计算的一个重要环节，它直接影响动力计算结果的精度。自振周期的计算方法有很多，如解析法，集中质量法，广义坐标法及有限元法。

自振周期 - 自振周期折减系数由于计算模型的简化和非结构因素的作用，导致多层钢筋混凝土框架结构在弹性阶段的计算自振周期（下简称“计算周期”）比真实自振周期（下简称“自振周期”）偏长。因此，无论是采用理论公式计算还是经验公式计算；无论是简化手算还是采用计算机程序计算，结构的计算周期值都应根据具体情况采用自振周期折减系数（下简称“折减系数”）加以修正，经修正后的计算周期即为设计采用的实际周期（下简称“设计周期”），设计周期=计算周期×折减系数。如果折减系数取值不恰当，往往使结构设计不合理，或造成浪费、或甚至产生安全隐患。诚然，折减系数是钢筋混凝土框架结设计所需要解决的一个重要问题。 影响自振周期因素是诸多方面的，加之多层钢筋混凝土框架结构实际工程的复杂性，抗震规范[1]没有、也不可能对折减系数给出一个确切的数值。许多文献中给出，当主要考虑填充墙的刚度影响时，折减系数可取0.6~0.7[4] [7]；根据填充墙的多少、填充墙开洞情况，其对结构自振周期影响的不同，可取0.50~0.90[2].这些都是以粘土实心砖为填充墙的经验值，不言而喻，采用不同填充墙体材料的折减系数是不相同的。当采用轻质材料或空心砖作填充墙，当然不应该套用实心砖为填充墙的折减系数。对于粘土实心砖外的其它墙体可根据具体情况确定折减系数。2

自振周期 - 结构周期关系按照行业标准《工程抗震术语标准》（JGJ/97）的有关条文， 自振周期：结构按某一振型完成一次自由振动所需的时间。 基本周期：结构按基本振型（第一振型）完成一次自由振动所需 的时间。通常需要考虑两个主轴方向和扭转方向的基本周期。

设计特征周期 ：抗震设计用的地震影响系数曲线的下降段起始点所对应的周期值，与地震震级、震中距和场地类别等因素有关。

场地卓越周期：根据场地覆盖层厚度H和土层平均剪切波速 ，按公式T=4H/ 计算的周期，表示场地土最主要的振动特征。 结构在地震作用下的反应与建筑物的动力特性密切相关，建筑物的自振周期是主要的动力特征，与结构的质量和刚度有关，当自振周期、特别是基本周期小于或等于设计特征周期 时，地震影响系数取值为 ，按规范计算的地震作用最大。

国内外的震害经验表明，当建筑物的自振周期与场地的卓越周期相等或相近时，地震时可能发生共振，建筑物的震害比较严重。研究表明，由于土在地震时的应力-应变关系为非线性的，在同一地点，地震时场地的卓越周期并不是不变的，而将因震级大小、震源机制、震中距离的变化而不同。

GB50011规范对结构的基本周期与场地的卓越周期之间的关系不做具体要求，即不要求结构自振周期避开场地卓越周期。事实上，多自由度结构体系具有多个自振周期，不可能完全避开场地卓越周期。

本词条内容贡献者为:

刘玉峰 - 副教授 - 辽宁大学