置信度传播(英语:belief propagation),又称为乘积和信息传递(sum-product message passing),是在贝叶斯网络、马尔可夫随机场等概率图模型中用于推断的一种信息传递算法。
简介在给定已观测节点时,可以用该算法高效地计算未观测节点的边缘分布。置信度传播在人工智能、信息论中十分常见,已成功应用于低密度奇偶检查码、Turbo码、自由能估计、可满足性等不同领域。
历史置信度传播由美国计算机科学家朱迪亚·珀尔于1982年提出。最初该算法的运用范围仅限于树,不久则扩展到多树。此后,研究者发现在一般的图中该算法是一种十分有用的近似算法。1
置信度传播基础贝叶斯网络贝叶斯网络(Bayesian network),又称信念网络(belief network)或是有向无环图模型(directed acyclic graphical model),是一种概率图型模型,借由有向无环图(directed acyclic graphs, or DAGs)中得知一组随机变量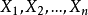 及其n组条件概率分布(conditional probability distributions, or CPDs)的性质。举例而言,贝叶斯网络可用来表示疾病和其相关症状间的概率关系;倘若已知某种症状下,贝叶斯网络就可用来计算各种可能罹患疾病之发生概率。
及其n组条件概率分布(conditional probability distributions, or CPDs)的性质。举例而言,贝叶斯网络可用来表示疾病和其相关症状间的概率关系;倘若已知某种症状下,贝叶斯网络就可用来计算各种可能罹患疾病之发生概率。
一般而言,贝叶斯网络的有向无环图中的节点表示随机变量,它们可以是可观察到的变量,抑或是隐变量、未知参数等。连接两个节点的箭头代表此两个随机变量是具有因果关系或是非条件独立的;而两个节点间若没有箭头相互连接一起的情况就称其随机变量彼此间为条件独立。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是“果(descendants or children)”,两节点就会产生一个条件概率值。比方说,我们以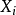 表示第i个节点,而
表示第i个节点,而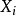 的“因”以
的“因”以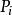 表示,
表示,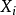 的“果”以
的“果”以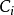 表示;图一就是一种典型的贝叶斯网络结构图,依照先前的定义,我们就可以轻易的从图一可以得知:
表示;图一就是一种典型的贝叶斯网络结构图,依照先前的定义,我们就可以轻易的从图一可以得知:
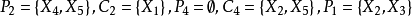 ,以及
,以及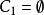
大部分的情况下,贝叶斯网络适用在节点的性质是属于离散型的情况下,且依照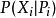 此条件概率写出条件概率表(conditional probability table, or CPT),此条件概率表的每一行(row)列出所有可能发生的
此条件概率写出条件概率表(conditional probability table, or CPT),此条件概率表的每一行(row)列出所有可能发生的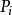 ,每一列(column)列出所有可能发生的
,每一列(column)列出所有可能发生的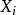 ,且任一行的概率总和必为1。写出条件概率表后就很容易将事情给条理化,且轻易地得知此贝叶斯网络结构图中各节点间之因果关系;但是条件概率表也有其缺点:若是节点
,且任一行的概率总和必为1。写出条件概率表后就很容易将事情给条理化,且轻易地得知此贝叶斯网络结构图中各节点间之因果关系;但是条件概率表也有其缺点:若是节点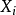 是由很多的“因”所造成的“果”,如此条件概率表就会变得在计算上既复杂又使用不便。2
是由很多的“因”所造成的“果”,如此条件概率表就会变得在计算上既复杂又使用不便。2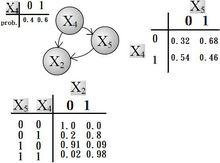
马尔可夫网络马尔可夫网络,(马尔可夫随机场、无向图模型)是关于一组有马尔可夫性质随机变量{\displaystyle X}的全联合概率分布模型。
马尔可夫网络类似贝叶斯网络用于表示依赖关系。但是,一方面它可以表示贝叶斯网络无法表示的一些依赖关系,如循环依赖;另一方面,它不能表示贝叶斯网络能够表示的某些关系,如推导关系。马尔可夫网络的原型是易辛模型,最初是用来说明该模型的基本假设。
形式上,一个马尔可夫网络包括:
一个无向图G= (V,E),每个顶点v∈V表示一个在集合 X 的随机变量,每条边{u,v} ∈E表示随机变量u和v之间的一种依赖关系。
一个函数集合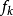 (也称为因子或者团因子有时也称为特征),每一个
(也称为因子或者团因子有时也称为特征),每一个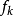 的定义域是图G的团或子团k. 每一个
的定义域是图G的团或子团k. 每一个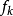 是从可能的特定联合的指派(到元素k)到非负实数的映射。1
是从可能的特定联合的指派(到元素k)到非负实数的映射。1
本词条内容贡献者为:
尹维龙 - 副教授 - 哈尔滨工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国