[科普中国]-狄利克雷形式

狭义的狄氏型是指定义在希尔伯特空间的一个稠密子空间D(E)上的、满足一定条件的双线性泛函E。

简介狄利克雷形式亦称狄氏型。

狭义的狄氏型是指定义在如下希尔伯特空间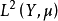的一个稠密子空间D(E)上的、满足一定条件的双线性泛函E，即(Y,𝒥)是一个可测空间，μ是(Y,𝒥)上σ有限测度，Y上定义的、关于μ平方可积的数值函数（等价类）全体关于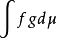为内积构成的希尔伯特空间记为L2(Y,μ)。1

希尔伯特空间在数学中，希尔伯特空间是欧几里德空间的一个推广，其不再局限于有限维的情形。与欧几里德空间相仿，希尔伯特空间也是一个内积空间，其上有距离和角的概念（及由此引申而来的正交性与垂直性的概念）。

此外，希尔伯特空间还是一个完备的空间，其上所有的柯西序列等价于收敛序列，从而微积分中的大部分概念都可以无障碍地推广到希尔伯特空间中。希尔伯特空间为基于任意正交系上的多项式表示的傅立叶级数和傅立叶变换提供了一种有效的表述方式，而这也是泛函分析的核心概念之一。希尔伯特空间是公式化数学和量子力学的关键性概念之一。

泛函泛函是数学中重要的基本概念，是现代数学的重要研究对象之一，也是数学与其它领域研究与应用的一个重要工具。泛函分析是研究拓扑线性空间到拓扑线性空间之间满足各种拓扑和代数条件的映射的分支学科。

它是20世纪30年代形成的。从变分法、微分方程、积分方程、函数论以及量子物理等的研究中发展起来的，它运用几何学、代数学的观点和方法研究分析学的课题，可看作无限维的分析学。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所