[科普中国]-极小边界

极小边界（minimal boundary）是极小细拓扑下的边界。布雷洛(Brelot,M.E.)还考虑了更一般的极小瘦与极小边界。

简介极小瘦在考虑抽象调和锥时，Ω的子集E称为关于极小调和函数h(h≠0)为瘦，指的是关于凸锥∑，h到E的简化函数R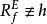。集族{Ω\E|E关于h瘦}构成一个滤子𝓕h；令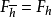，它是类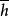中所有的极小调和函数(≠0)所对应的共同滤子。

定义关于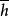，全体m作为Ω的抽象边界称为极小边界，它是极小细拓扑下的边界。

背景布雷洛(Brelot,M.E.)还考虑了更一般的极小瘦与极小边界。1

抽象边界抽象边界由不属于指定的拓扑空间Ω的点组成的集合，是Ω在延拓后的拓扑空间内的边界。

具体地，在非空集合Ω上赋予拓扑𝒥，设I是非空指标集，若对每个i∈l，对应着一个由开集组成的滤基𝓑i，则在Ω∪I上存在满足下述条件的拓扑𝒥1：

1.𝒥1在Ω的诱导拓扑为𝒥；

2.对任意i∈l，Ω与i的邻域的交全体构成由𝓑i生成的滤子。

于是关于𝒥1，I是Ω的边界，称之为Ω的抽象边界。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所