[科普中国]-仿傅里叶积分算子

仿傅里叶积分算子是现代微分算子理论中的一种重要的算子。F(p)在仿微分算子理论中有许多与傅里叶积分算子在拟微分算子理论中相似的性质。

简介仿傅里叶积分算子是现代微分算子理论中的一种重要的算子。

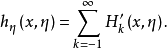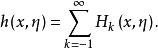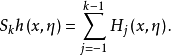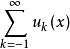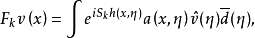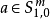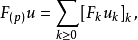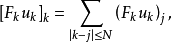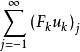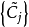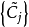设h(x,η)∈Cρ+1(Rn×Rn\{0})是关于η为正齐一次的实函数，且它具非异的黑塞矩阵，p>0，所以h(x,η)=⟨η,hη(x,η)⟩，取hη(x,η)的李特尔伍德-佩利分解，且限制于Sn-1上，然后对η进行零次延拓，可得令Hk(x,η)=⟨η,h'k(x,η)⟩，它关于η为正齐一次，且是C∞函数。故记又设u(x)的李特尔伍德-佩利二进分解为，做傅里叶积分算子Fk：其中，且为简单计，设它关于x支集。于是可定义仿傅里叶积分算子F(p)为其中而是Fkuk的李特尔伍德-佩利二进分解；对应的环体是，2N是中与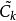相交的环体的个数。

性质F(p)在仿微分算子理论中有许多与傅里叶积分算子在拟微分算子理论中相似的性质。特别地，也有叶戈罗夫相似性定理。于是就有可能对仿微分算子进行微局部化简。

用此方法可以再次证明邦尼(Bony,J.M.)的奇性传播定理，且可给出具有常重特征的非线性的低频情况下弱奇性的传播定理，从而显示出它在重特征非线性奇性传播中的潜力。1

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学