拉德马赫函数系是有重要力量和应用价值的一个特殊正交函数系。拉德马赫函数系的函数在二进区间上取值1,-1或0,它与在应用中有重要意义的沃尔什函数系关系密切。
简介拉德马赫函数系是有重要力量和应用价值的一个特殊正交函数系。
在一维情形,可先定义函数
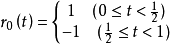 然后将
然后将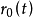 按周期 1 做延拓,即令
按周期 1 做延拓,即令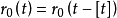 ([t]为 t 的整数部分)或
([t]为 t 的整数部分)或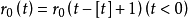 ,再定义
,再定义
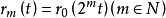 则
则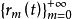 称为区间 [0,1]上的拉德马赫函数系,它是[0,1]上的正交系,但不是完备的。
称为区间 [0,1]上的拉德马赫函数系,它是[0,1]上的正交系,但不是完备的。
性质拉德马赫函数系有如下重要性质:
设数列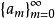 有
有
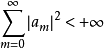 则级数
则级数
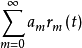 在[0,1]上几乎处处收敛,其和
在[0,1]上几乎处处收敛,其和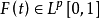 对一切
对一切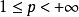 成立;还存在正的常数 Ap和Bp,使
成立;还存在正的常数 Ap和Bp,使
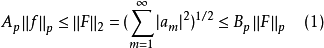 因此
因此
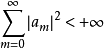 可用以刻画
可用以刻画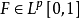 。
。
应用拉德马赫函数系的函数在二进区间上取值1,-1或0,它与在应用中有重要意义的沃尔什函数系关系密切,在应用中常称为开关函数,是由德国数学家拉德马赫于1922年提出的,还有一些等价的定义方式(例如可表示成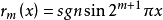 ,这里sgn表示符合函数)。
,这里sgn表示符合函数)。
推广拉德马赫函数系可以推广到高维空间,记
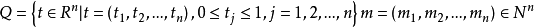 则由
则由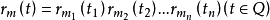 定义的函数系
定义的函数系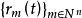 可称为 Q 上的拉德马赫函数系,它具有与一维情形相同的性质的重要意义,特别地,若将
可称为 Q 上的拉德马赫函数系,它具有与一维情形相同的性质的重要意义,特别地,若将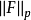 和
和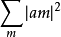 分别理解成
分别理解成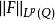 和
和
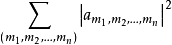 则由
则由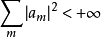 仍有
仍有
 并且(1)式(其中各有关量均按n维情形定义)仍然成立。1
并且(1)式(其中各有关量均按n维情形定义)仍然成立。1
本词条内容贡献者为:
胡启洲 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国