[科普中国]-变动边界变分问题

自由横截性条件建立了平稳曲线的切线斜率与曲线λ的切线斜率的关系，这里的自由端在曲线λ上移动，称为变动端点，相应变分问题称为变动边界变分问题。

简介自由横截性条件自由横截性条件是由变分为零导出的极值函数在变动边界上满足的条件。

设泛函

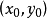为固定端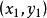，为变动端，在曲线λ上移动，λ的斜率为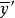，极值曲线的自由横截性条件为

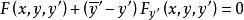
定义自由横截性条件建立了平稳曲线的切线斜率与曲线λ的切线斜率的关系，这里的自由端在曲线λ上移动，称为变动端点，相应变分问题称为变动边界变分问题。1

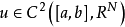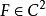实例对于一元向量值函数，若，u是

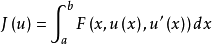的极小函数（或平稳点），(b,u(b))固定，而(a,u(a)) 在RN+1中的正则曲面ℳ上移动，ℳ:G(x,z)=0，则曲线z=u(x)和曲面ℳ 在曲线的左端点P1=(a,u(a)) 自由横截，即满足下列横截性条件：

1、G(a,u(a))=0,即P1∈ℳ；

2、向量 𝒩(a)=(F-u'·Fp,Fp)|x=a 正交于ℳ在P1的切空间Tpℳ。

变动边界横截性条件变动边界的横截性条件称为自由横截性条件。

例如，设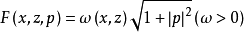，则 z=u(x)和ℳ在x=a 的自由横截性条件就是曲线 z=u(x) 与曲面ℳ 在P1=(a,u(a)) 的正交性。这是因为

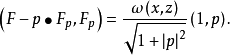
本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学