柳斯捷尔尼克-施尼雷尔曼重数定理是利用畴数对流形上泛函的临界点的个数进行估计的重要定理。
简介柳斯捷尔尼克-施尼雷尔曼重数定理是利用畴数对流形上泛函的临界点的个数进行估计的重要定理。
设M是完备的巴拿赫-芬斯勒流形,f∈C1(M,R)满足(P.S)条件,对每个n=1,2,...,记𝓕k= {A⊂M|A闭,CatM(A)≥k}。令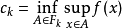 (约定当Fk= ∅时,ck=+∞)。若对某个正整数k与p,有-∞
(约定当Fk= ∅时,ck=+∞)。若对某个正整数k与p,有-∞
柳斯捷尔尼克-施尼雷尔曼重数定理是利用畴数对流形上泛函的临界点的个数进行估计的重要定理。
简介柳斯捷尔尼克-施尼雷尔曼重数定理是利用畴数对流形上泛函的临界点的个数进行估计的重要定理。
设M是完备的巴拿赫-芬斯勒流形,f∈C1(M,R)满足(P.S)条件,对每个n=1,2,...,记𝓕k= {A⊂M|A闭,CatM(A)≥k}。令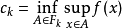 (约定当Fk= ∅时,ck=+∞)。若对某个正整数k与p,有-∞
(约定当Fk= ∅时,ck=+∞)。若对某个正整数k与p,有-∞
 扫码下载APP
扫码下载APP

