[科普中国]-中心平稳曲线场

中心平稳曲线场（central field of stationary curve）是从一固定点出发的平稳曲线构成的场。

简介中心平稳曲线场是从一固定点出发的平稳曲线构成的场。

设M0是空间的一个定点，由这一点引出泛函

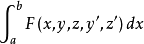的平稳曲线束，它们在M0的某个邻域内成为平稳曲线簇，在每一条平稳曲线上取一点M，使在所有平稳曲线上弧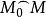的 J-长度等于同一个数ρ，这样的平稳曲线簇称为中心平稳曲线场。

推广点 M 的几何轨迹是一个曲面，这个曲面为场的横截曲面，即平稳曲线簇与横截曲面横截相交，沿平稳曲线上弧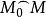的 J 长度是点 M 的函数，记为θ(x,y,z)=ρ，称为θ(x,y,z)为中心平稳曲线场的基本函数，由横截曲面方程与横截条件

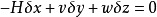可以推出

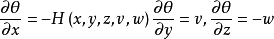由上述三个方程中消去v，w，就得到场的基本函数的一阶偏微分方程，称为哈密顿-雅可比方程：

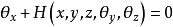
性质对一般情形，设Ω是R×RN中一区域，F(x,z,p)在Ω×RN上属C3，而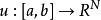是泛函

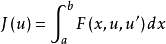的平稳函数，对所有 是可逆的，又设[a,b]不包含 u 的成对共轭值，则可把 u 嵌入到中心平稳曲线场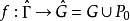，P0是结点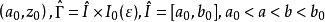

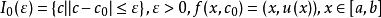
f 在 的限制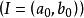是 G=f(Γ)上的迈尔场。1

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学