[科普中国]-博特定理

博特定理是同伦群的周期性定理，是关于从球面到复数域上一般线性群的连续映射性质的一个定理。

简介博特定理是同伦群的周期性定理，是关于从球面到复数域上一般线性群的连续映射性质的一个定理。

设Sn-1为Rn中的单位球面，GL(N,C)是从CN到CN上线性映射（从而是双射）所构成的一般线性群，于是博特(Borr,R.)的一个定理说，对于连续映射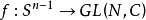 ，当2N≥n时：

若n为奇数，则f同伦于常值映射。

若n为偶数，对于每个f可以定义一个整数deg(f)，使得：

1、f同伦于g，当且仅当deg(f)=deg(g)；

2、对于任意给定的整数m，存在一个连续映射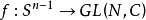 ，使得deg(f)=m。

同伦论中的定义按照同伦论的术语，博特定理可以被陈述为：当2N≥n时GL(N,C)的同伦群为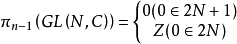 由此可知，GL(N,C)的同伦群之间有关系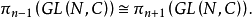

由此可见，这是一种周期性的定理。1

同伦群(homotopy groups)

同伦群是基本群的高维推广，1维同伦群就是基本群π1(X,x0)。

当拓扑空间是道路连通空间时，其同伦群与基点选取无关;利用连续映射诱导的同伦群之间同态的一些性质得出，同伦群是同伦型不变量（更是拓扑不变的）；当n≥2时，同伦群πn(X,x0)是交换群，因而有时把运算写成[α]+[β]。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所