[科普中国]-马肯厚普条件

马肯厚普条件是对使哈代-李特尔伍德极大算子M为加权Lp有界的权函数的特征刻画。

简介概述马肯厚普条件亦称 Ap 条件，是对使哈代-李特尔伍德极大算子M为加权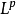有界的权函数的特征刻画。

具体内容设 10,使对Rn 中任意立方体Q及Q中任意勒贝格可测集E，有

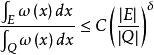其中|E|表示 E的勒贝格测度。1

哈代-李特尔伍德极大算子设f在R上局部可积（即在R的每个紧子集上都可积），若函数为f的哈代-李特尔伍德极大函数，则映射M:f→M(f)称为哈代-李特尔伍德极大算子。

哈代-李特尔伍德极大算子M在调和分析中的重要作用在于它能在一定意义下控制许多算子。因此极大算子M在算子有界性的研究中起着十分重要的作用。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学