[科普中国]-高斯-外尔斯特拉斯平均

高斯-外尔斯特拉斯平均（Uauss-Weierstrassmean）是多重傅里叶级数的一种重要的线性求和。

简介高斯-外尔斯特拉斯平均是多重傅里叶级数的一种重要的线性求和。

设f∈L(Tn)，f的傅里叶级数的高斯-外尔斯特拉斯平均是

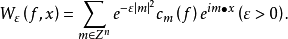
性质当ε→0时，高斯-外尔斯特拉斯平均既按Lp范数收敛于f∈Lp(Tn)，也在f的每个勒贝格点x处收敛于f(x)。1

傅里叶级数的线性求和傅里叶级数的线性求和是用线性算子对傅里叶级数的求和法。

从已给的傅里叶级数出发，构造新的三角级数或三角多项式，使之与所给的函数之间保持着线性的对应关系，这种构造新三角级数或三角多项式的方法称为傅里叶级数的线性求和法。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学