[科普中国]-惠特尼覆盖引理

惠特尼覆盖引理（Whitney covering lemma）是覆盖引理的一种形式。

简介惠特尼覆盖引理是覆盖引理的一种形式。1

设Ω为Rn中的开集，且|Ω|0}i，使得下列性质成立：

1、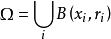 ，但 为一列互不相交的球。

2、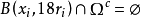 ，但 。

3、存在常数M=M(n)，满足

覆盖覆盖是数学术语。

设Ф是拓扑空间X的子集族，称Ф是X的一个覆盖，如果对任意x∈X，x至少包含在Ф的一个成员之中。

维塔利-维纳覆盖引理维塔利-维纳覆盖引理是覆盖引理的一种形式。

设区域Ω⊂Rn，且|Ω|0，使得球B(x,r(x))⊂Ω，则存在序列{B(xi,r(xi))}i，使得诸球B(xi,r(xi))互不相交，且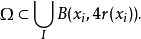

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学