[科普中国]-复微分p形式

丛ΛpCT*(M)的截面就称为M上的复微分p形式（complex differential p-form），p≥0。

简介复微分p形式是一种截面。

丛ΛpCT*(M)的截面就称为M上的复微分p形式，p≥0。1

性质外微分复化后给出复微分形式上的算子，仍记为d，算子d的性质与实流形的外微分运算的性质相同，此外它是实的，即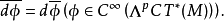

截面当需要考察对末态的运动参量加某种限制时的截面变化率，这就导致微分截面的概念。例如在弹性散射中，在空间某特定方向单位立体角的散射截面就是一种描写角分布的微分截面。

当需要考察对末态进行不连续变化的分类截面时，就导致部分截面的概念。例如在研究散射问题时，当把散射过程按碰撞角动量来分解，则截面就可表示成各种角动量对截面贡献之和，这种给定角动量的截面就是一种部分截面。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所