[科普中国]-弗洛伊德定理

弗洛伊德定理是最佳逼近算子的连续性定理。弗洛伊德(Freud,G.)在1958年还证明了这个算子在每点都满足李普希茨条件。

简介弗洛伊德定理是最佳逼近算子的连续性定理。

设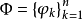在[a,b]上满足哈尔条件，f∈C[a,b]。记f关于Φ中的最佳逼近广义多项式为𝒯f，则𝒯是C[a,b]到C[a,b]中的一个连续算子。

性质弗洛伊德(Freud,G.)在1958年还证明了最佳逼近算子在每点都满足李普希茨条件，也即对于每个f0∈C[a,b]，都存在常数λ>0，使得对所有的f∈C[a,b]，都成立着||𝒯f0-𝒯f||≤λ||f0-f||。1

最佳逼近(best approximation)

最佳逼近是最小的逼近偏差。

设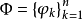，φk∈C[a,b]，称具有实系数ak的线性组合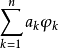为关于Φ的广义多项式。对于f∈C[a,b]，用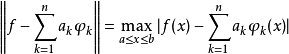表示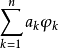对f的逼近偏差。称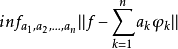为关于Φ的广义多项式对f的最佳逼近值，或简称最佳逼近，也称最佳一致逼近。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学