[科普中国]-哈尔条件

哈尔条件是代数多项式零点性质的一个扩充。哈尔条件的等价形式是每个φk(x)都在[a,b]上连续并且每n个形如(φ1(x),φ2(x),...,φn(x))的向量的集合都线性无关。

简介哈尔条件是代数多项式零点性质的一个扩充。

设φk∈C[a,b](k=1,2,...,n)，称函数组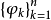在[a,b]上满足哈尔条件，是指其不恒为零的关于Φ的广义多项式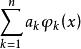在[a,b]上至多有n-1个零点，其中ak(k=1,2,...,n)是任意给定的实数。

等价形式哈尔条件的等价形式是每个φk(x)都在[a,b]上连续并且每n个形如(φ1(x),φ2(x),...,φn(x))的向量的集合都线性无关。

换句话说，称函数组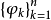在[a,b]上满足哈尔条件，是指每个函数φk(x)在[a,b]上都连续并且由[a,b]上n个相异的点x1,x2,...,xn做成的行列式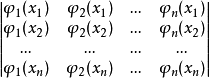都不等于0。1

零点零点，对于函数y=f(x)，使f(x)=0的实数x叫做函数y=f(x)的零点，即零点不是点。

这样，函数y=f(x)的零点就是方程f(x)=0的实数根，也就是函数y=f(x)的图象与x轴的交点的横坐标。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学