[科普中国]-杰克森定理

杰克森定理是用函数的构造性刻画其最佳逼近值的阶的定理，是杰克森(Jackson,D.)在1912年建立的。

简介杰克森定理是用函数的构造性刻画其最佳逼近值的阶的定理。

这是杰克森(Jackson,D.)在1912年建立的，人们称之为杰克森定理。

具体内容设f∈C[a,b]，ω(f,δ)是f的连续性模，En(f)是n次代数多项式对f的最佳逼近值，则有 如果f∈C[a,b]有r阶连续导数f(r)∈C[a,b]，那么这里Cr是一个仅与r有关的正数。1

最佳逼近值记πn为次数不高于n的代数多项式a0+a1x+...+anx的全体，这里ak(k=0,1,...,n)是实数。对于函数f∈C[a,b]，称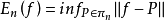 为n次代数多项式对f在[a,b]上的最佳逼近值（度），也简称最佳逼近。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学