[科普中国]-循环卷积

循环卷积(circular convolution) 不同于线性卷积的一种卷积运算，是周期卷积的一种。

定义计算两个长度均为N的序列x1(n)和x2(n)的循环卷积，一个简易的办法是先把x1(n)的数据，设x1(n)=(1，2，3，4)，N=4，按反时针方向均匀分布在一个圆周上。如图1中(a)。的内圆所示，而把x2(n)，设x2(n)={5，6，7，8}，按顺时针的方向均匀分布在另一个同心圆上，然后求两圆上相应序列的乘积，并把V项乘积叠加起来作为n=0时刻的卷积值y(0)，即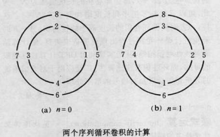

y(0)=1×5+4×6+3×7+2×8=66

若求n=1时刻的y(l)值，可将外圆的：x2(n)固定，把内圆上的序列x1(n)顺时针旋转一个单位时间（或将x1(n)固定，把外圆上的序列x2(n)逆时针旋转），然后把对应项的乘积叠加起来，即为所求。如(b)图所示，即

y(1)=2×5+1×6+4×7+3×8=68

这样依次将内圆序列进行循环移位一周，便可以求得：y(2)=66，y(3)=60。所以循环卷积又称圆周卷积，卷积结果y(n)长度仍等于N，其定义式如图2。方括号内的运算代表两个周期序列的周期卷积。它与线性卷积不同之处是卷积过程只限在m=0到N-1的一个周期内。乘以RN(n)表示卷积结果只取长度为N的主值序列。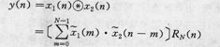

由于离散傅里叶变换(DFT)的实质是周期序列变换到频域的描述。可以证明：两个有限长序列在时域的循环卷积，其DFT等于在频域两个序列相应的DFT的乘积。1

式中X1(k)和x2(k)分别是x1(n)和x2(n)的N点DFT。它表明DFT具有循环卷积性质（CCP），也是区别于其他变换的重要特性。正是这种性质，用计算机通过计算DFT达到计算循环卷积和线性卷积的目的，提髙了运算效率。按长度为N的两个序列，其线性卷积的长度应为2N-1，而循环卷积的长度仍然为N。为此，可以通过补零把序列长度增加到L≥2N-1。这样，一方面使循环卷积的长度等于线性卷积，另一方面避免进行循环卷积过程出现混叠造成失真，使计算结果与线性卷积相等，从而实现利用DFT计算线性卷积的目的。循环卷积有快速算法，广泛应用于对通信系统的分析和综合以及对信号的数字处理。

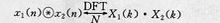
线性卷积对于线性非时变离散时间系统来说，若序列x(n)是系统的输入，h(n)是系统在单位脉冲作用下的单位脉冲响应，则由于输入序列x(n)可表示为一系列脉冲的线性组合，所以，根据线性系统的叠加性质，系统的输出在系统初始不储能的条件下(零状态响应)可由图4式求得.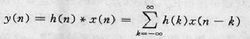

上式在运算过程存在序列的翻转、移位、相乘和相加，所以称为卷积和。x(n)*h(n)表示两个序列相卷积的运算符号，故式①也就是卷积的定义式。为了与离散傅里叶变换的循环卷积以及周期序列的周期卷积相区别，通常所指的卷积又称为线性卷积。卷积运算符合交换率，可写成另一种等效形式如图5.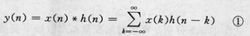

线性卷积的计算可以用解析法，也可以用图解法。若两 个序列的长度分别为N1和N2，则卷积结果的总长度应为L=N1+N2-1。

同理，对线性非时变连续系统来说，若连续时间信号x(t)是系统的输入，h(t)是系统在单位脉冲作用下的单位冲激响应，则系统在零状态的输出为它们的卷积积分

线性卷积是数字信号处理中最常见的一种基本运算，不仅用于系统分析还用于系统设计。如果代表滤波器的脉冲响应则卷积运算就是一种线性滤波，y(n)是信号x(n)通过滤波器后的响应。

循环卷积和线性卷积的关系在实际问题中，碰到的问题大多数是求解线性卷积，例如，一个LSI系统，输出y(n)为y(n)=x(n)*h(n)

下面将看到在一定条件下，可用循环卷积代替线性卷积，今后可看到循环卷积比线性卷积在计算速度上可提高许多倍。

设 x(n)是长度为 N 的有限长序列， h(n)是长度为 M 的有限长度序列。2

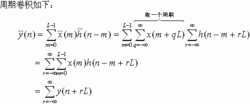
意义循环卷积是使用DFT(FFT)计算线性卷积时的衍生品。首先连续时间没有循环卷积概念。离散时间时，不妨假设x(n)为L点信号， 仅在0~L-1有非零值；h(n)为M点信号，仅在0~M-1有非零值。以x(n)为输入信号通过以h(n)为单位冲激响应的线性时不变系统得到输出 y(n) = x(n) * h(n)，线性卷积，直接计算的复杂度为 O(LM)1。

本词条内容贡献者为:

鄢志丹 - 副教授 - 中国石油大学（华东）