[科普中国]-时频分析

时频分布是一项让我们能够同时观察一个讯号的时域和频域资讯的工具，而时频分析就是在分析时频分布。传统上，我们常用傅里叶变换来观察一个讯号的频谱。然而，这样的方法不适合用来分析一个频率会随着时间而改变的讯号。

简介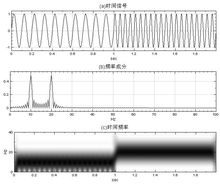时频分析（JTFA）即时频联合域分析（Joint Time-Frequency Analysis）的简称，作为分析时变非平稳信号的有力工具，成为现代信号处理研究的一个热点，它作为一种新兴的信号处理方法，近年来受到越来越多的重视。时频分析方法提供了时间域与频率域的联合分布信息，清楚地描述了信号频率随时间变化的关系。

时频分析的基本思想是：设计时间和频率的联合函数，用它同时描述信号在不同时间和频率的能量密度或强度。时间和频率的这种联合函数简称为时频分布。利用时频分布来分析信号，能给出各个时刻的瞬时频率及其幅值，并且能够进行时频滤波和时变信号研究。1

常见的时频分布函数常见的时频分布函数有短时距傅里叶变换（包含加伯转换）、科恩分布函数（包含韦格纳分布）、改进型韦格纳分布，以及加伯-韦格纳分布（Gabor-Wigner distribution function）函数及S转换等。1

重要性（1）时间和频率是描述信号的两个最重要的物理量。

（2）信号的时域和频域之间具有紧密的联系。

（3）检测微小信号，不漏掉信号。1

主要方法（1）短时傅立叶变换（Gabor变换）；

（2）连续小波变换；

（3）Wigner-Ville分布 ；

（4）希尔伯特黄变换（Hilbert-Huang Transform，HHT ）；

（5）S变换以及广义S变换1

应用可以利用线性完整转换来任意的改变一个讯号在时频分布平面上面的形状和位置，像是水平以及垂直的移动、扩大、shearing（扭曲），以及旋转（用分数傅里叶变换，fractional Fourier transform, FRFT）等。由此可见，线性完整转换让我们对于时频分布的处理更灵活。1

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学