[科普中国]-环形折积

环形折积与线性折积类似，皆是针对两个函数的运算子。假设两个函数分别为f与g，则折积运算过程即为将其中一个函数(如f)经过翻转后，对于每个位移量，将重叠的部分相乘累加起来(见下文定义)。不同的地方在于环形折积的位移为环形位移，而线性折积的位移为平移。折积亦可以视为滑动平移的推广。

简介环形折积与线性折积类似，皆是针对两个函数的运算子。假设两个函数分别为f与g，则折积运算过程即为将其中一个函数(如f)经过翻转后，对于每个位移量，将重叠的部分相乘累加起来(见下文定义)。不同的地方在于环形折积的位移为环形位移，而线性折积的位移为平移。折积亦可以视为滑动平移的推广。

定义两个函数的环形折积定义为对一个或两个函数做周期延伸后之折积运算，而所谓的周期延伸是指原来的函数平移固定长度的整数倍再全部加起来所产生的新函数。x(t)经过周期延伸后之函数可写成下式:

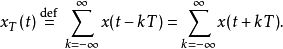其中T为周期(即周期延伸中的固定长度)

对x(t)与h(t)计算环形折积的运算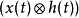可以下列两种等价表示式定义:

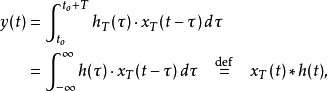其中*****表示线性折积运算子

此两定义的等价关系证明如下:

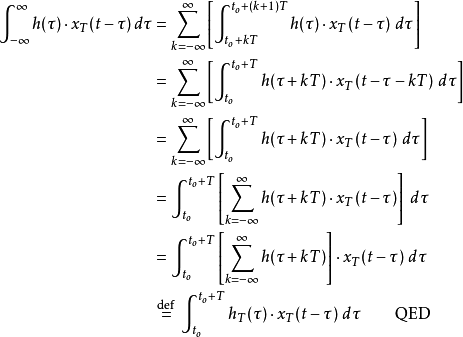
上述为针对两个连续信号(函数)的环形折积之定义的说明，类似的，我们对于周期为N的离散信号之环形折积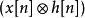有如下的定义:

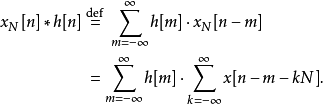
离散信号的环形折积可以结合快速傅立叶变换与折积理论做相当有效率的计算，然而，在实际上信号处理或系统理论的应用，线性折积运算较常被考虑也较有物理意义，于是，如果可将一个线性折积的计算问题转化为求算环形折积，则一般当两个输入信号长度相距不远时，往往计算量可以大为减少，增加了计算线性折积的效率，至于线性折积与环形折积的关系以及如何利用环形折积与傅立叶变换求得线性折积结果。1

区块折积当计算折积之两信号长度相差很大时，利用快速傅立叶变换计算折积是较没有效率的，此时较有效率的方法是将较长的信号切成一段段的区块，以此每一区块对另一输入信号进行折积再合并，常见的区块折积方法包括重叠-相加之折积法与重叠-储存之折积法，针对长度的不同，区块长度的选取亦会影响计算的效率。1

相关条目折积

离散傅立叶变换

区块折积

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学