[科普中国]-谐波分析

简谐运动处理起来是比较简单的，但是很多振动系统的运动却不是简谐的。然而，很多情况下的振动是周期的，任何关于时间的周期函数都能展开成傅立叶级数，即无限多个正弦函数和余弦函数的和表示，我们将这种分析方法称为谐波分析。

简介起源“谐波”一词起源于声学。有关谐波的数学分析在18世纪和19世纪已经奠定了良好的基础。傅里叶等人提出的谐波分析方法仍被广泛应用。

电力系统的谐波问题早在20世纪20年代和30年代就引起了人们的注意。当时在德国，由于使用静止汞弧变流器而造成了电压、电流波形的畸变。1945年J.C.Read发表的有关变流器谐波的论文是早期有关谐波研究的经典论文。 到了50年代和60年代，由于高压直流输电技术的发展，发表了有关变流器引起电力系统谐波问题的大量论文。70年代以来，由于电力电子技术的飞速发展，各种电力电子装置在电力系统、工业、交通及家庭中的应用日益广泛，谐波所造成的危害也日趋严重。世界各国都对谐波问题予以充分的关注。国际上召开了多次有关谐波问题的学术会议，不少国家和国际学术组织都制定了限制电力系统谐波和用电设备谐波的标准和规定。1

意义谐波的危害十分严重——谐波使电能的生产、传输和利用的效率降低，使电气设备过热、产生振动和噪声，并使绝缘老化，使用寿命缩短，甚至发生故障或烧毁。谐波可引起电力系统局部并联谐振或串联谐振，使谐波含量放大，造成电容器等设备烧毁。谐波还会引起继电保护和自动装置误动作，使电能计量出现混乱。对于电力系统外部，谐波对通信设备和电子设备会产生严重干扰。

谐波危害（1）谐波使公用电网中的元件产生了附加的谐波损耗，降低了发电、输电及用电设备的效率，大量的3次谐波流过中性线时会使线路过热甚至发生火灾。

（2）谐波影响各种电气设备的正常工作。谐波对电机的影响除引起附加损耗外，还会产生机械振动、噪声和过电压，使变压器局部严重过热。谐波使电容器、电缆等设备过热、绝缘老化、寿命缩短，以至损坏。

（3）谐波会引起公用电网中局部的并联谐振和串联谐振，从而使谐波放大，这就使上述（1）和（2）的危害大大增加，甚至引起严重事故。

（4）谐波会导致继电保护和自动装置的误动作，并会使电气测量仪表计量不准确。

（5）谐波会对邻近的通信系统产生干扰，轻者产生噪声，降低通信质量；重者导致住处丢失，使通信系统无法正常工作。

分析方法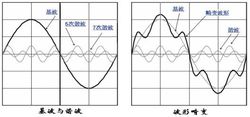满足一定条件（Dirichlet条件）的、以T为周期的时间的周期函数f(t)，在连续点处，可用下述的三角函数的线性组合（傅里叶级数）来表示：

上式称为f(t)的傅里叶级数，其中，ω=2π/T。

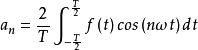n为整数，n>=0。

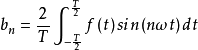
n为整数，n>=1。

在间断点处，下式成立：

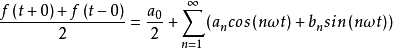a0/2为信号f(t)的直流分量。

令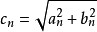

c1为基波幅值，cn为n次谐波的幅值。c1有时也称1次谐波的幅值。a0/2有时也称0次谐波的幅值。

非正弦波里含有大量的谐波，不同的波形里含有不同的谐波成份。在倍频器、变频器里，就必须要进行谐波分析，分柝各次谐波的分布；在乐器、音响、放大器……也要分析谐波成份。

（1）奇次谐波，指频率为基波频率的3、5、7……倍的谐波；

（2）偶次谐波，指频率是基波频率的2、4、6……倍的谐波。

对f(t)=-f(t+T/2) 的函数(T为函数周期)，偶次谐波及直流分量为0；

对f(t)=f(t+T/2) 的函数(T为函数周期)， 奇次谐波为0。

测量方法谐波分析是信号处理的一种基本手段。在电力系统的谐波分析中，主要采用各种谐波分析仪分析电网电压、电流信号的谐波，该类仪表的谐波分析次数一般在40次以下。

对于富含谐波的变频器输出的PWM波，其谐波主要集中在载波频率的整数倍附近，当载波频率高于基波频率40倍时，采用上述谐波分析设备，其谐波含量近似等于零，不能满足谐波分析的需要。

上述场合，当载波频率固定时，谐波的频率范围相对固定，而所需分析的谐波次数，与基波频率密切相关，基波频率越低，需要分析的谐波次数越高。一般宜采用宽频带的，运算能力较强、存储容量较大的变频功率分析仪，根据需要，其谐波分析的次数可达数百甚至数千次。例如，当载波频率为2kHz，基波频率为50Hz时，其40次左右的谐波含量最大；当基波频率为5Hz时，其400次左右的谐波含量最大，需要分析的谐波次数一般至少应达到2000次。

同时，选择仪表的同时，还应选择合适带宽的传感器，因为传感器的带宽将限制进入二次仪表的信号的有效带宽。一般用选择宽频带的电压、电流传感器，如：变频功率传感器。

凯塞窗插值FFT的电力谐波分析与应用研究背景高精度谐波分析对电能计量、谐波潮流计算、电力系统谐波补偿与抑制等有重要意义。采用快速傅里叶变换(fastFouriertransform，FFT)算法进行谐波分析，非整周期截断时产生频谱泄漏和栅栏效应，影响谐波分析精度。针对FFT算法的不足，国内外学者提出了一系列加窗插值FFT算法。V.K.Jain等提出基于矩形窗的插值算法，可有效提高计算精度。此后，Hanning窗、Blackman-Harris窗、Rife-Vincent(I)窗、Nuttall窗和矩形卷积窗等被提出并被运用到FFT谐波分析中。基于余弦组合窗的插值FFT算法、基于矩形窗的多谱线插值算法和采用多项式拟合的双谱线插值方法等高精度插值FFT算法相继被提出，提高了谐波分析精度。

采用矩形窗、三角窗等基本窗函数和广义余弦窗函数对信号加权，对于动态信号分析效果受到窗函数固定旁瓣性能的制约。Kaiser窗可定义一组可调的窗函数，其主瓣能量和旁瓣能量的比例近乎最大，且可自由选择主瓣宽度和旁瓣高度之间的比重。研究对信号在整周期截断和非整周期截断时的频谱进行分析，讨论Kaiser窗的频谱特性，提出基于Kaiser窗插值FFT的电力谐波分析算法，建立奇次、偶次谐波求解的数学模型和实用的插值修正公式，推导信号基波与各次谐波频率、幅值和初相角计算式，采用包含21次谐波的动态信号仿真和三相谐波电能表应用实践进一步证明研究方法的有效性和准确性。

实际应用基于本文提出的基于Kaiser窗插值FFT的电力谐波分析方法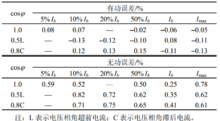设计的三相多功能谐波电能表研制成功后，在湖南省电力公司计量中心进行了大量的试验与测试检验。

实验选择基波功率叠加15次谐波功率为例。其中，基波电压为220V，基波电流为1.5A。基波电压叠加谐波电压：U3=10%，U5=9%，U7=7%，U9=5%，U11=3%，U13=2%，U15=1%。基波电流叠加谐波电流：I3=20%，I5=15%，I7=12%，I9=10%，I11=8%，I13=7%，I15=5%，各次谐波相位差均为20°。标准源采用为JCD4060三相精密谐波源。

表1给出比差角差校正后的基波功率误差数据。图1、2分别给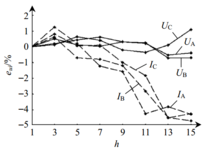出比差角差校正后ABC三相各次谐波电压与谐波电流的误差数据、基波功率因数cosϕ分别为1.0与0.5L时各次谐波相位的误差数据。

由表1和图1、2可知，测量准确度达到基波有功的相对误差≤0.2%，基波无功的相对误差≤1%，各次谐波电压的相对误差≤2%，各次谐波电流的相对误差≤5%，谐波相位测量的绝对误差≤5°，满足A类谐波测量仪器标准GB/T14549—1993。

研究结论采用矩形、三角窗等基本窗函数和广义余弦窗函数对信号加权可减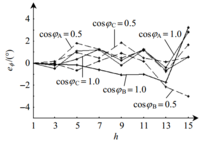少非整数周期截断造成的频谱泄漏和栅栏效应影响，但其效果受到窗函数固定旁瓣性能的制约。Kaiser窗可定义一组可调的窗函数，自由选择主瓣与旁瓣衰减之间的比重，因此能全面反映主瓣与旁瓣衰减之间的交换关系。本文根据Kaiser窗良好的频谱泄漏抑制特性，结合FFT进行电力谐波分析，提出了基于Kaiser窗插值FFT算法，对包含21次谐波的动态信号仿真和三相多功能谐波电能表实际应用表明，采用本文提出的基于Kaiser窗插值FFT电力谐波分析方法，具有较高的计算精度，且设计灵活、实用价值高，据此实现的三相多功能谐波电能表准确度达0.2S级，2~21次谐波分析满足GB/T14549—1993的A类谐波测量仪器要求。2

本词条内容贡献者为:

胡芳碧 - 副教授 - 西南大学