[科普中国]-缺省逻辑

缺省逻辑是 Ray Reiter 提出的用来形式化有缺省假定的推理的非单调逻辑。 缺省逻辑可以表达像“缺省的，某个事物是真的”的事实；相反的，标准逻辑只能表达某个事物为真或某个事物为假。这是一个问题，因为推理经常涉及在多数时候是真但不总是真的事实的推理。经典的例子是： “鸟通常会飞”。这个规则可以在标准逻辑中表达为要么“所有鸟都会飞”，这与企鹅不会飞的事实相矛盾；要么“除了企鹅、鸵鸟 ... 的所有鸟都会飞”，这要求规则指定出所有的例外。缺省逻辑致力于形式化像这样的推理规则，而不需要明确提及所有的例外。

缺省逻辑的变体缺省逻辑的下列变体同最初的语法和语义二者有所区别。

断言变体：断言是由一个公式和一个公式的集合构成的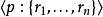对。这种对指示P是真，当公式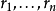已经被假定为一致于证明P为真的时候。一个断言缺省理论由叫做背景理论的断言理论（断言公式的集合）和按原始语法定义的缺省的集合构成。当一个缺省应用于断言理论的时候，把由它的结论和它的论据合成的对增加到这个理论。下列语义使用了断言理论：

积累缺省逻辑

委托假定缺省逻辑

准缺省逻辑

弱扩展：不再检查前件在由背景理论和已应用的缺省的结论构成的理论中是否是有效的，检查前件在将要生成的扩展中的有效性；换句话说，生成扩展的算法开始于猜测一个理论并使用它代替背景理论；从扩展生成的过程得到的结果实际上是一个扩展，只在它等价于在开始时所猜测的理论的时候。缺省逻辑的这个变体在原理上与自动认识逻辑有关，在那里理论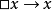 有一种模型，在其中x是真，只是因为假定 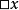为真，公式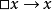 支持这个初始假定。

析取缺省逻辑：缺省的结论是公式的集合而不是单一的公式。在应用缺省的时候，至少其中一个结论被非确定性的选择为真。

缺省上的优先级：可以明确的指定缺省的相对优先级；在可以应用于一个理论的缺省之间，只有最高优先级的可以应用。缺省逻辑的某些语义不要求明确指定优先级；而是更多特殊性（在更少情况下可应用的）缺省优于更少特殊性的缺省。

统计变体：统计缺省对缺省附加错误频率的上限；换句话说，缺省被假定为是不正确的推理规则，应用它的次数到了这个分数的时候。

转换缺省理论可以被转换成其他逻辑的理论或反之。转换要考虑下列条件：

结论保持：最初和转换后的理论有同样的（命题）结论；

忠实：这个条件有意义只在如下转换的时候，在缺省逻辑的两个变体之间、或在缺省逻辑和在其中类似于扩展的概念比如模态逻辑中模型存在的逻辑之间；一个转换是忠实的，如果在最初和转换后的理论的扩展（或模型）之间存在一个映射（典型的是双射）；

模块化：从缺省逻辑到其他逻辑的转换是模块化的，如果缺省和背景理论可以分开转换；此外，向背景理论增加公式只导致向转换的结果增加新公式；

同字母表：最初和转换后的理论建立在相同的字母表之上；

多项式：转换的运行时间和生成的理论的大小要求是最初理论的多项式。

转换典型的要求忠实或至少是结论保持，而模块化和同字母表的条件有时被忽略。

在命题缺省逻辑和下列逻辑之间的转换已经研究过了：

经典命题逻辑；

自动认识逻辑；

限定于被正规理论的命题缺省逻辑；

缺省逻辑的可作为替代的语义；

界限。

转换存在与否依赖于施加那种条件。从命题缺省逻辑到经典命题逻辑的转换不能总是生成多项式大小的命题理论，除非多项式层次瓦解。到自动认识逻辑的转换存在与否依赖于是否要求模块性或使用相同的字母表。1

复杂性关于缺省逻辑的下列问题的计算复杂性是已知的：

扩展的存在性：决定一个命题缺省理论是否有至少一个扩展是{\displaystyle NP^{NP}}-完全的；

怀疑的蕴涵：决定一个命题缺省理论是否怀疑的蕴涵一个命题公式是{\displaystyle co-NP^{NP}}-完全的；

轻信的蕴涵：决定一个命题缺省理论是否轻信的蕴涵一个命题公式是{\displaystyle NP^{NP}}-完全的；

扩展检查：决定一个命题公式是否等价于一个命题缺省理论的扩展是{\displaystyle P^{NP[log]}}-完全的；

模型检查：决定一个命题释义是否是一个命题缺省理论的扩展的模型是{\displaystyle NP^{NP}}-完全的。

实现有两个系统实现了缺省逻辑：DeReS和XRay。2

本词条内容贡献者为:

黎明 - 副教授 - 西南大学