[科普中国]-平性凸赋范线性空间

平性凸赋范线性空间（flat convex normed linear space）是一类赋范线性空间。

简介平性凸赋范线性空间是一类赋范线性空间。1

赋范线性空间(X,||·||)称为是平性凸的，如果存在单位向量x0,y0(x0≠y0)，使得

赋范线性空间赋范线性空间(normed linear space)是在线性空间中引进一种与代数运算相联系的度量，即由向量范数诱导出的度量。赋范线性空间称为Banach空间，是指由范数导出的度量是完备的。

设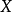是线性空间，函数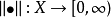称为上定义的一个范数，如果满足：

（1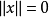）当且仅当；

（2）对任何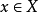及，；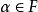

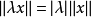（3）对任意，。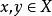

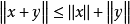称二元体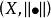为赋范线性空间。

单位向量单位向量是指模等于1的向量。由于是非零向量，单位向量具有确定的方向。

一个非零向量除以它的模，可得所需单位向量。设原来的向量是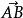，则与它方向相同的的单位向量；

一个单位向量的平面直角坐标系上的坐标表示可以是：(n,k) ，则有n²+k²=1。其中k/n就是原向量在这个坐标系内的所在直线的斜率。这个向量是它所在直线的一个单位方向向量。不同的单位向量，是指它们的方向不同。对于任意一个非零向量a，与它同方向的单位向量记作。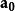

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学