[科普中国]-线性卷积

线性卷积(linear convolution) 在时域描述线性系统输入和输出之间关系的一种运算。这种运算在线性系统分析和信号处理中应用很多，通常简称卷积。中文名：数字信号处理

定义对于线性非时变离散时间系统来说，若序列x(n)是系统的输入，h(n)是系统在单位脉冲作用下的单位脉冲响应，则由于输入序列x(n)可表示为一系列脉冲的线性组合，所以，根据线性系统的叠加性质，系统的输出在系统初始不储能的条件下(零状态响应)可由图1式求得。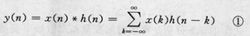

上式在运算过程存在序列的翻转、移位、相乘和相加，所以称为卷积和。x(n)*h(n)表示两个序列相卷积的运算符号，故式①也就是卷积的定义式。为了与离散傅里叶变换的循环卷积以及周期序列的周期卷积相区别，通常所指的卷积又称为线性卷积。卷积运算符合交换率，可写成另一种等效形式。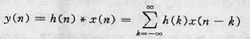

线性卷积的计算可以用解析法，也可以用图解法。若两 个序列的长度分别为N1和N2，则卷积结果的总长度应为L=N1+N2-1。

同理，对线性非时变连续系统来说，若连续时间信号x(t)是系统的输入，h(t)是系统在单位脉冲作用下的单位冲激响应，则系统在零状态的输出为它们的卷积积分。

线性卷积是数字信号处理中最常见的一种基本运算，不仅用于系统分析还用于系统设计。如果代表滤波器的脉冲响应则卷积运算就是一种线性滤波，y(n)是信号x(n)通过滤波器后的响应。

基本理论线性卷积是对线性移不变（LSI）系统的输入输出关系的描述，体现系统的特性。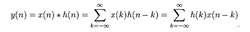

线性卷积的表达式为图3，一般情况，现实的系统为因果系统，有k=max(N1,N2)，定义它们的N点圆周卷积为如图6。

圆周卷积与线性卷积之间的关系：当有限长序列x(n)和h(n)的长度分别为N1和N2，取N>=max(N1,N2)，当N>=N1+N2-1，则线性卷积与圆周卷积相同。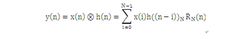

对于线性卷积，一般直接比较麻烦，由上可知当取点数足够多时（点数不够补零），可求解圆周卷积即可，而圆周卷积又可通过FFT实现，从而实现线性卷积通过FFT和IFFT实现。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院