[科普中国]-詹姆斯空间

詹姆斯空间是詹姆斯(James,R.C.) 于1951年针对当时关于“巴拿赫空间X等距同构于X**推出X必自反”的猜测而构造的空间。

简介詹姆斯空间是詹姆斯(James,R.C.) 于1951年针对当时关于“巴拿赫空间X等距同构于X**推出X必自反”的猜测而构造的空间。

设 J 为满足下述条件的实数列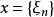 所组成的实线性空间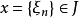： 当且仅当

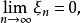并且

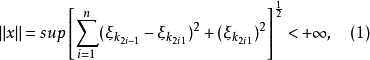其中上确界对一切 n 级所有可能的有限多个正整数取的；由(1) 所规定的‖·‖ 为 J 上的范数，并且按此范数构成一个巴拿赫空间。巴拿赫空间 J 称为詹姆斯空间。

推论由詹姆斯空间的定义有以下结论：

1.J为可分的巴拿赫空间。

2.J与J**等距同构,但J并不自反。

因此，在巴拿赫空间自反性的定义中必须强调在自然（典则）映射下，X=X**。

应用泛函分析中许多反例的构造常用到詹姆斯空间。1

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学