[科普中国]-重要性采样

重要性采样（英语：importance sampling）是统计学中估计某一分布性质时使用的一种方法。该方法从与原分布不同的另一个分布中采样，而对原先分布的性质进行估计。重要性采样与计算物理学中的伞形采样相关。

简介重要性采样是蒙特卡洛方法中的一个重要策略。该方法不改变统计量，只改变概率分布，可以用来降低方差1。

重要性采样算法就是在有限的采样次数内，尽量让采样点覆盖对积分贡献很大的点。

目标其目标是用一种受控的方式改变仿真，以便增加稀少事件的数目，同时还能正确地确定解调差错概率。常规重要性采样（CIS）是一种降方差的仿真方法，它通过提供有偏噪声来实现，等效于使系统工作在一个较低的信噪比环境下。

原理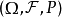假设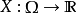为概率空间上的一个随机变量。我们想要估计X的期望值，记作E[X;P]。如果根据P随机抽取样本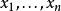，估计的期望值即12

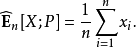
这一估计的精确度取决于X的方差，

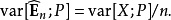
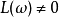而重要性采样的基本思想则是从另一个分布中抽取样本，用以降低E[X;P]估计的方差。进行重要性采样时，首先选择一个随机变量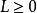，使得E[L;P]=1，并满足P上几乎处处。由此，可以定义新的概率

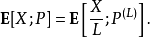
于是，我们可以从P上抽样，通过变量X/L估计E[X;P]。如果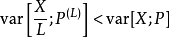成立，此时的估计便优于直接在原分布上采样得到的估计。

当X在Ω上不变号时，最优的L为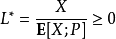。此时X/L*即为要估计的E[X;P]，只需一个样本便可得到该值。然而由于L*与要估计的E[X;P]有关，在实际操作中我们无法取到理论上最优的L*。不过，我们仍可以采用如下方式逼近该理论值：

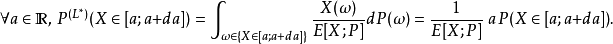
于是，要估计的期望值可改写为：

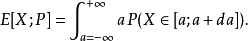
注意到，更优（即让估计值方差更小）的P会使得样本分布的频率与其在E[X;P]计算中的权重更加相关。这也是该方法得名“重要性采样”的原因。

重要性采样常用于蒙特卡洛积分。当P为均匀分布、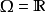时，E[X;P]即为实函数的积分。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学