[科普中国]-紧支撑映射

紧支撑映射是一种具有紧致基本集的映射。如果f具有一个相对于M的紧支撑集，则称f是相对于M的紧支撑映射。

简介紧支撑映射是一种具有紧致基本集的映射。

设X是巴拿赫空间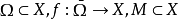，。若X的一个非空有界闭凸集C满足下述条件：

1.C包含f相对于M的一个闭基本集；

2.f(C∩M)⊂C；

3.f在C∩M上全连续，则称C为f相对于M的一个支撑。

如果f具有一个相对于M的紧支撑集，则称f是相对于M的紧支撑映射。

应用紧支撑映射常用到的情形是，Ω是X中的有界开集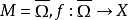，连续。这时，若f是（严格）集压缩映射，或凝聚映射，或终归紧映射，则f是Ω上的紧支撑映射。

若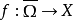是紧支撑映射，则I-f称为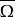上的紧支撑向量场。1

基本集基本集是动力系统研究的重要不变集之一。它是根据公理A系统谱分解的基本集所具有的动力学性质而抽象出来的概念。

在动力系统的研究中，对基本集的理解一般认为它不是单独的一个双曲不动点(双曲奇点)。基本集的作用在于它在很大程度上确定了系统的轨道结构。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院