[科普中国]-酉膨胀

酉膨胀是将某一希尔伯特空间上的算子按一定条件膨胀为另一更大的希尔伯特空间上的酉算子。

简介酉膨胀是将某一希尔伯特空间上的算子按一定条件膨胀为另一更大的希尔伯特空间上的酉算子。

酉膨胀的数学形式是，是否存在希尔伯特空间H'⊃H，以及H'上酉算子U，使得，其中P是H'到H上的正交投影。

如果存在如此的(H',U)，则称(H',U)是T的酉膨胀。这样的算子T必定是压缩算子。

实例复希尔伯特空间H上每个压缩算子T都存在酉膨胀，例如取H'= H⊕H,

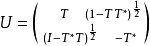除酉等价外压缩算子的酉膨胀是惟一的。1

酉算子酉变换是泛函分析和算子理论中的一个重要概念，傅里叶变换就是酉变换之一例。酉算子又叫保范算子，它是欧式空间中旋转概念在无穷维情况下的推广；希尔伯特空间的酉算子是仍保持其内积意义的希尔伯特空间的线性变换。酉算子具有逆算子，其逆算子也是一种酉算子，且酉算子和其逆算子是一对共轭算子。n阶复方阵U的n个列向量是U空间的一个标准正交基，则U是U矩阵；一个简单的充分必要判别准则是方阵U的转置共扼距阵乘以U 等于单位阵，则U是U矩阵。

压缩算子压缩算子是对任何点的范数都不放大的一类线性算子，又称为收缩算子。收缩算子在研究微分方程不动点理论和计算方法中的一类迭代算法的误差估计起重要作用。

设X,Y是赋范线性空间，T是X到Y的线性算子，如果对一切x∈X，满足||Tx||≤||x||，则称T收缩算子或压缩算子。

T是收缩算子的充分必要条件是T的范数||T||≤1。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院