[科普中国]-形变引理

形变引理指在巴拿赫流形上利用泛函的伪梯度向量场对泛函的水平集进行所需形变的一些定理。

简介形变引理是研究临界点的有力工具，指在巴拿赫流形上利用泛函的伪梯度向量场对泛函的水平集进行所需形变的一些定理。

内容形变引理方面的结果很多，下述是其中之一。

设M是完备的C2-0芬斯勒流形，f∈C1(M,R)满足(P.S)条件，设c∈R，Kc={x∈M|df(x)=0,f(x)=c}。U是K的开邻域，则存在M上的合痕η:[0,1]×M→M与两个正常数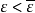，使得：

1、。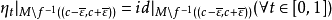

2、。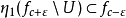

3、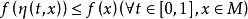，其中对实数b，fb={x∈M|f(x)≤b}。

特别地，当Kc=∅时，取U=∅，则上述2成为η1(fc+ε)⊂fc-ε。1

伪梯度向量场(pseudo-gradient vector field)

伪梯度向量场是梯度向量场在不适合用来构造下降流时的一种替代物。

伪梯度向量场的概念及其存在性最早由帕莱斯(Palais,R.S.)于1966年给出。

当M是一般巴拿赫流形，f∈C2-0(M,R)时，余切向量场df不能用来构造下降流；

当M是希尔伯特流形而f∈C1(M,R)时梯度向量场∇f也不能用来构造下降流。伪梯度向量场是克服这两种困难的工具。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学