[科普中国]-拟相似线性算子

设A,B是巴拿赫空间上的有界线性算子，如果存在两个有稠密值域的单射的线性算子T和S，使得TA=BT，AS=SB成立，则称A和B拟相似。

简介拟相似线性算子是相似线性算子的推广。

设A,B是巴拿赫空间上的有界线性算子，如果存在两个有稠密值域的单射的线性算子T和S，使得TA=BT，AS=SB成立，则称A和B拟相似。1

相似线性算子相似线性算子是相似矩阵的推广，相似算子具有相同的谱。

设A,B是巴拿赫空间上的有界线性算子，如果存在可逆的有界算子W（即W,W-1都有界），使得B=W-1AW，则称A和B相似。

有界线性算子有界线性算子是泛函分析中一种重要的算子。

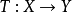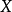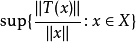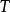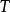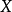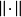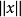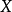设是从线性赋范空间到的线性算子。 如果当存在且有限，则称是有界线性算子，也就是说将中的每个有界集映射为中的有界集。此处|表示范数，表示中定义的范数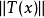，表示中定义的范数。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院