[科普中国]-共鸣定理

共鸣定理亦称一致有界性原理或巴拿赫-施坦豪斯定理，是论述有关一族有界线性算子为一致有界的定理。

简介共鸣定理亦称一致有界性原理或巴拿赫-施坦豪斯定理，是论述有关一族有界线性算子为一致有界的定理。

共鸣定理断言：设X是巴拿赫空间，Y是赋范线性空间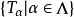， 是从X到Y的一族有界线性算子，如果对每个x∈X都有

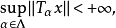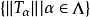则数集 是有界的。

发展共鸣定理是泛函分析中的一条重要定理，它是由巴拿赫(Banach,S.)与施坦豪斯(Steinhaus,H.D.)于1927年在勒贝格(Lebesgue,H. l.)关于奇异积分、特普利茨(Toeplitz,O.)关于正则求和法以及哈恩(Hahn,H.) 关于插值理论等前人研究成果的基础上提出的。1

有界线性算子有界线性算子是泛函分析中一种重要的算子。

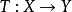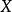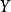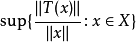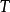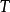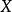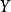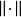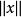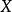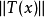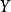设是从线性赋范空间到的线性算子。 如果当存在且有限，则称是有界线性算子，也就是说将中的每个有界集映射为中的有界集。此处|表示范数，表示中定义的范数，表示中定义的范数。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院