可逆线性算子是一种具有有界逆映射的线性算子,是线性代数中可逆矩阵概念的一种推广。
简介可逆线性算子是一种具有有界逆映射的线性算子,可逆线性算子是线性代数中可逆矩阵概念的一种推广。
设X,Y是赋范线性空间,T是线性算子,𝓓(T)⊂X,𝓡(T)⊂Y。如果𝓡(T)=Y,T是一对一的,且T-1有界,则称T是可逆线性算子。1
线性算子线性算子是线性空间之间保持线性运算的映射。
设X,Y同是数域K上的线性空间,D是X的线性子空间,T是从D到Y中的映射。如果对每个x,y∈D,有T(x+y)=Tx+Ty,则称T是可加算子。如果对每个x∈D和实数α有T(αx)=αTx,则称T是实齐次的,如果对一切a∈K这个关系式都成立,则称T是齐次算子。
如果T既是可加的又是齐次的,则称T是线性算子或线性映射,D称为T的定义域,常记为𝒟(T)。
当𝒟(T)=X时,称T是X到Y的线性算子。特别地,当Y=K(或Y是一维线性空间)时,T称为D上的线性泛函。线性泛函是线性算子的特殊情形。
可逆矩阵矩阵A为n阶方阵,若存在n阶矩阵B,使得矩阵A、B的乘积为单位阵,则称A为可逆阵,B为A的逆矩阵。若方阵的逆阵存在,则称为可逆矩阵或非奇异矩阵,且其逆矩阵唯一。
设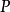 是数域,
是数域,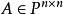 ,若存在
,若存在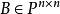 ,使得
,使得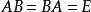 ,
,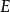 为单位阵,则称
为单位阵,则称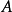 为可逆阵,
为可逆阵, 为
为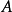 的逆矩阵,记为
的逆矩阵,记为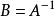 。若方阵
。若方阵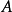 的逆阵存在,则称
的逆阵存在,则称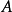 为可逆矩阵或非奇异矩阵。
为可逆矩阵或非奇异矩阵。
本词条内容贡献者为:
李宗秀 - 副教授 - 黑龙江财经学院




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国