高阶弗雷歇微分亦称高阶强微分,简称高阶F微分或高阶微分,是 F 微分概念的高阶推广形式。
简介高阶弗雷歇微分亦称高阶强微分,简称高阶F微分或高阶微分,是 F 微分概念的高阶推广形式。
一阶 F 微分设 X,Y为赋范线性空间,Ω 是 X 中的开集,f:Ω→Y,x0∈Ω。归纳定义f 在x0的n阶F微分,记为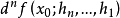 。一阶 F 微分
。一阶 F 微分 ,即F微分已有定义。
,即F微分已有定义。
定义设 f 在x0的某邻域中有n阶F微分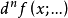 ,若存在有界(n+1)线性算子
,若存在有界(n+1)线性算子
 使得对任意对
使得对任意对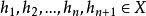 ,有
,有
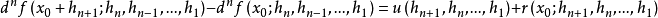 其中
其中
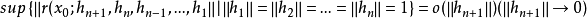 则
则 称为 f 在x0的(n+1) 阶 F 微分,记为
称为 f 在x0的(n+1) 阶 F 微分,记为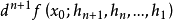 。1
。1
弗雷歇微分弗雷歇微分简称F微分,亦称强微分,是数学分析中全微分概念和变分法中强变分概念的推广。
强可微的概念是由弗雷歇于1910年引入的。
设X,Y为赋范线性空间,Ω是X中的开集,f:Ω→Y是映射,x0∈Ω。若存在有界线性算子A:X→Y ,使得f(x0+h)-f(x0)-Ah=o(||h||),其中o(||h||)/||h||→0(当||h||→0),则称 f 在x0弗雷歇可微(简称F可微)或强可微,A称为f在x0的弗雷歇导算子(简称F导算子)或强导算子,记为df(x0)或f'(x0),Ah称为f在x0沿h的F微分或强微分,记为df(x0;h)或f'(x0)h。
本词条内容贡献者为:
李宗秀 - 副教授 - 黑龙江财经学院




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国