[科普中国]-弗雷歇-泰勒公式

弗雷歇-泰勒公式（Frechet-Taylor formula）是经典的泰勒公式在F微分意义下的推广。

简介弗雷歇-泰勒公式是经典的泰勒公式在F微分意义下的推广。1

设 X 和Y是巴拿赫空间，Ω是 X 的开凸子集，x0∈Ω，f:Ω→Y。若 f 在Ω上存在 n 阶 F导算子 f(n)，则对任意的h∈X，x0+h∈Ω，成立下述泰勒公式

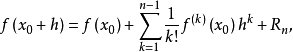且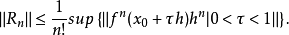

推论若f(n) 在Ω上还是连续的，则有

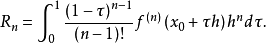
泰勒公式数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式，是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。

若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶导数，且在开区间(a,b)上具有n+1阶导数，则对闭区间[a,b]上任意一点x，成立下式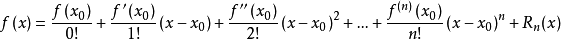：其中，f(x)表示f(x)的n阶导数，等号后的多项式称为函数f(x)在x0处的泰勒展开式，剩余的Rn(x)是泰勒公式的余项，是(x-x0)n的高阶无穷小。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院