[科普中国]-可微函数芽环

可微函数芽环(ring of germs of differentiablefunctions)是一种特殊的环。指可微函数芽的全体在以自然方式定义的加法、乘法下构成的环。考虑n维欧氏空间R上的无穷次可微函数在原点O的芽，以记号f：(R，0)→R记之。

概念可微函数芽环(ring of germs of differentiablefunctions)是一种特殊的环。指可微函数芽的全体在以自然方式定义的加法、乘法下构成的环。考虑n维欧氏空间R上的无穷次可微函数在原点O的芽，以记号f：(R，0)→R记之。以ε(n)记这样的芽的全体做成的集合，并以自然的方式在其上定义函数芽的相加、相乘以及函数芽与实数的相乘。对于这些运算，ε(n)成为具有单位元的交换环，且是R上的代数，称为可微函数芽环或称可微函数芽代数。ε(n)中那些在原点取值为0的芽之全体做成ε(n)的惟一极大理想，记为m(n)。这个极大理想m(n)在奇点理论研究中起着重要的作用。1

函数芽函数芽是奇点理论与突变理论的主要研究对象之一。确定在一点的邻域上的连续映射的等价类。精确地说，设X，Y是拓扑空间，p∈X，考虑由在点p附近定义的全体连续映射g所构成的集合A，A={g|g：U→Y，U是点p的开邻域，g是连续映射}。在这个集合里引进等价关系如下：设g：U→Y，f：V→Y是A中的两个映射，若存在点p的开邻域W，使得WU∩V，而且f和g在W上的限制相等，即f|W=g|W，则称f和g等价。在这个等价关系下的一个等价类就称为映射在点p的芽。常记为h：(X，p)→Y。这个类中的任何映射g都称为芽h的代表，而h也称为映射g在点p的芽。关于映射的许多概念，如两个映射的复合映射等都可以自然的方式搬到映射芽上来。特别地，函数的相乘、相加等概念能够以自然的方式搬到函数芽上。在奇点理论与突变理论中研究的是可微映射芽。

环环是对并与差运算封闭的集类，测度论中重要概念之一。设F是Ω上的一个非空集类。如果它对集的并及差运算封闭，即对任何A，B∈F，都有A∪B∈F，A\B∈F，则称F为Ω上的环。例如，若F是由实直线R上任意有限个左开右闭的有限区间的并集：

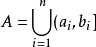的全体构成的集类，则F是R上的一个环。环也是对于交与对称差运算封闭的集类，并按这两种运算成为布尔环。要把R上的勒贝格测度和勒贝格-斯蒂尔杰斯测度以及相应的积分理论推广到更一般的集合上，就需要做一系列奠基工作，其中之一是建立一些特殊的集类并研究其性质。环以及半环、σ环、代数、σ代数等重要集类正是为了这一目的而引入的。2

奇点理论一门新兴的数学学科，它处在拓扑学、代数几何、微分几何、代数学、分析学等众多数学领域的交界处。追溯其历史渊源，有20世纪30年代，莫尔斯(Morse，M.)的临界点理论；20世纪40年代，惠特尼(Whitney，H.)的有关微分流形嵌入、浸入的奇点的工作；以及庞特里亚金(Понтрягин，Л.С.)与惠特尼等人的与示性类有关的奇点方面的工作。这是奇点理论的萌芽时期。1955年，惠特尼关于平面映到平面的映射的奇点的工作，标志着奇点理论开始作为一个独立的数学分支登上了数学舞台。1956年，托姆(Thom，R.)的论文《可微映射的奇点》，对奇点理论做了高度的概括，为其以后的发展提出了纲领式的描述；1960年，他在波恩做了系列演讲，使其纲领式的描述更加具体化。此后，奇点理论得到了蓬勃的发展，一方面奇点理论本身取得了重大进展，如玛瑟(Mather，J.N.)关于稳定性方面与阿诺尔德(Арнольд，В.И.)关于奇点分类方面的工作；另一方面是奇点理论在自然科学中的应用也取得了重大的成就，这就是20世纪60年代末托姆创立的突变理论。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学