[科普中国]-芬斯勒度量

Fn上的芬斯勒度量是定义在切丛TFn上满足下列条件的连续的实值函数F。

简介芬斯勒度量是黎曼度量的一种推广。

若Fn是n维微分流形，TFn是Fn的切丛，Fn上的芬斯勒度量是定义在切丛TFn上满足下列条件的连续的实值函数F:设(x1,x2,...,xn)是Fn上局部坐标系，(x1,x2,...,xn;y1,y2,...,yn)是TFn的点(x,y)的局部坐标，其中(x1,x2,...,xn)是Fn的点x的局部坐标，(y1,y2,...,yn)是Fn的点x的切向量y的分量，即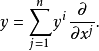

性质1、在y≠0，F(x,y)可微。

2、对任意实数λ，F(x,λy)=|λ|F(x,y)。

3、以为元素的矩阵是正定的。

此时，Fn称为芬斯勒空间，函数F也称为芬斯勒空间Fn的度量函数。以gij为分量的张量称为Fn的度量张量或基本张量，F(x,y)2称为基本形式。

当F(x,y)2是y1,y2,...,yn的二次齐式时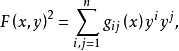，这个芬斯勒度量是黎曼度量。

判定微分流形上存在芬斯勒度量的充分必要条件是它为仿紧的。1

本词条内容贡献者为:

杨荣佳 - 教授 - 河北大学