[科普中国]-广义高斯-格林公式

广义高斯-格林公式（广义高斯-格林公式）是一般高斯-格林公式在测度积分形式下的推广。

简介广义高斯-格林公式是一般高斯-格林公式在测度积分形式下的推广。

高斯-格林公式利用密度概念可以定义的另一个重要概念是集合在一点处的外法线，当所论集合有光滑边界时，这个概念很直观，在一般情形则较为复杂。给定点集Q与测度v，可以定义一个新的测度v∟Q如下：对于集合G，规定G关于v∟Q的测度v∟Q(G)=v(Q∩G)。因此，Rn中集合A在一点b处的外法向量是如下定义的一个单位向量u=n(A,b)，它使得对于

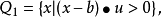
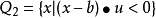有

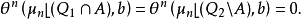
定义上述概念只含点集A关于μn的测度性质，而不需要预先知道A的几何性质，甚至连边界的概念也未提到，鉴于这样广义的概念，使人们可将古典的高斯-格林公式推广到相当一般的形式：设A为Rn中的子集，

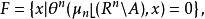
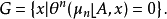
如果对于每个紧集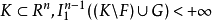，则对于Rn上每个有紧支集的李普希茨一阶向量场ξ，有

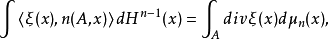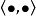此处表示内积。

另一方面，若以Bd A记A的普通边界，则当对于Rn中的每个紧集K，都有时，上述条件满足，从而上述广义高斯-格林定理成立。1

测度数学上，测度（Measure）是一个函数，它对一个给定集合的某些子集指定一个数，这个数可以比作大小、体积、概率等等。传统的积分是在区间上进行的，后来人们希望把积分推广到任意的集合上，就发展出测度的概念，它在数学分析和概率论有重要的地位。

**定义1：**构造一个集函数，它能赋予实数集簇М中的每一个集合E一个非负扩充实数mE。我们将此集函数称为E的测度。

**定义2：设Γ是集合X上一σ代数，ρ ：Γ →R∪{ +∽ }**是一集合函数，且ρ满足：

（1）（非负性）对任意的A∈Γ，有ρ(A)≧0;

（2）（规范性）ρ(Φ) = 0；

（3）（完全可加性） 对任意的一列两两不交集合A1，A2，……，An，……有ρ(∪n An)=∑n ρ（An）

则称ρ是定义在X上的一个测度，Γ中的集合是可测集，不在Γ中的集合是不可测集。特别的，若ρ(X) = 1 ，则称ρ为概率测度。

本词条内容贡献者为:

李华青 - 副教授 - 西南大学电子信息工程学院