[科普中国]-扩充实值集函数

若实值集函数的值可允许取+∞或-∞，则称此集函数为扩充实值集函数。

简介集函数集函数是测度论中定义的概念，是以集类为定义域的函数。

设𝒞是Ω上的一个集类，K是实数域或复数域，称映射μ:𝒞→K为定义在𝒞上的集函数。重要的（数值）集函数有测度、集上的积分等。

定义若实值集函数的值可允许取+∞或-∞，则称此集函数为扩充实值集函数。

性质关于集函数，也可引入单调性、收敛性等概念。

例如，设μ是定义在集类𝒞上的实值集函数，如果对任意A,B∈𝒞，A⊂B，均有μ(A)≤μ(B)，则说μ在𝒞上是单调增加的。

设{μn}是集类𝒞上的集函数列，若对于每个A∈𝒞，数列{μn(A)}收敛，则说{μn}在𝒞上收敛。若对于每个A∈𝒞，有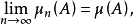 ，则称{μn}在𝒞上收敛于μ。

若对任意ε>0，存在正整数N，当n>N时，对一切A∈𝒞，都有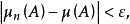则称{μn}在𝒞上一致收敛于μ。

向量值集函数当K是向量空间或算子集时，分别称映射μ:𝒞→K为𝒞上的向量值集函数或算子集函数。

常见的这种集函数有向量值测度、谱测度和谱积分等。1

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学