[科普中国]-高阶弱微分

高阶加托微分亦称高阶 G 微分或高阶弱微分，是 G 微分概念的高阶推广形式。

简介高阶加托微分亦称高阶 G 微分或高阶弱微分，是 G 微分概念的高阶推广形式。

二阶G可微设 X，Y为赋范线性空间，Ω是 X中的开集，f:Ω→Y是映射， 。若f 在Ω中每点 G 可微，则 ，在 有 G 微分 。这时若映射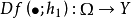 在x0为G可微，则称f 在x0为二阶G可微，映射 在x0沿方向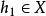 的G微分记为 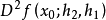，称为 f 在x0 点二阶G微分。

定义归纳地，若f在Ω中每点有n 阶G微分 在点x0为 G 可微，则称 f 在x0为n+1阶 G 可微，这时映射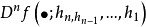 在x0沿hn+1点微分，记为 ，称为 f 在x0的n+1阶G微分。

推广如果 对每个变元 分别是线性的，则称 f 是x0有n阶线性微分，这时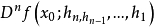 确定一n线性算子，记为 ，即有

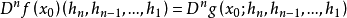
称为 f 在x0点n 阶加托导算子或n 阶G导算子或n 阶弱导算子，若还是有界的，则称 f 在x0有有界n阶线性G 微分。1

加托微分设X和Y是赋范线性空间，Ω是X中的开集，f:Ω→Y是映射，x0∈Ω。设h∈X，若极限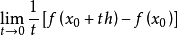存在，则该极限值称为映射f在点x0沿方向h的加托微分（或G微分）或弱微分，记为Df(x0;h)。

若f在x0沿任何方向h的弱微分均存在，则称f在点x0加托可微（或G可微）或弱可微。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院