[科普中国]-余切矢量场

余切矢量场即余切丛的截片。M上的余切矢量场指的是满足条件π𝜉=id的映射𝜉:M→T*M。

简介余切矢量场即余切丛的截片。

设为巴拿赫流形M的余切丛，M上的余切矢量场指的是满足条件π𝜉=id的映射𝜉:M→T*M（其中id为M上的恒同映射）。1

余切丛微分几何中，流形的余切丛是流形每点的切空间组成的向量丛。余切空间有一个标准的辛形式，从中可以一个余切丛的非退化的体积形式。因此，本身作为一个流形的余切丛总是可定向的。

可以在余切丛上定义一组特殊的坐标系；这些被称为标准坐标系。因为余切丛可以视为辛流形，任何余切丛上的实函数总是可以解释为一个哈密尔顿函数；这样余切丛可以理解为哈密尔顿力学讨论的相空间。

切向量场切向量场即切丛的截片，也常简称为向量场。

设M为巴拿赫微分流形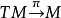，为其切丛，若Cr映射𝜉:M→TM满足条件π𝜉=id，其中id为M上的恒同映射，则称𝜉为M上的一个Cr切向量场。

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院